Предмет: Геометрия,
автор: meshalkinasonia
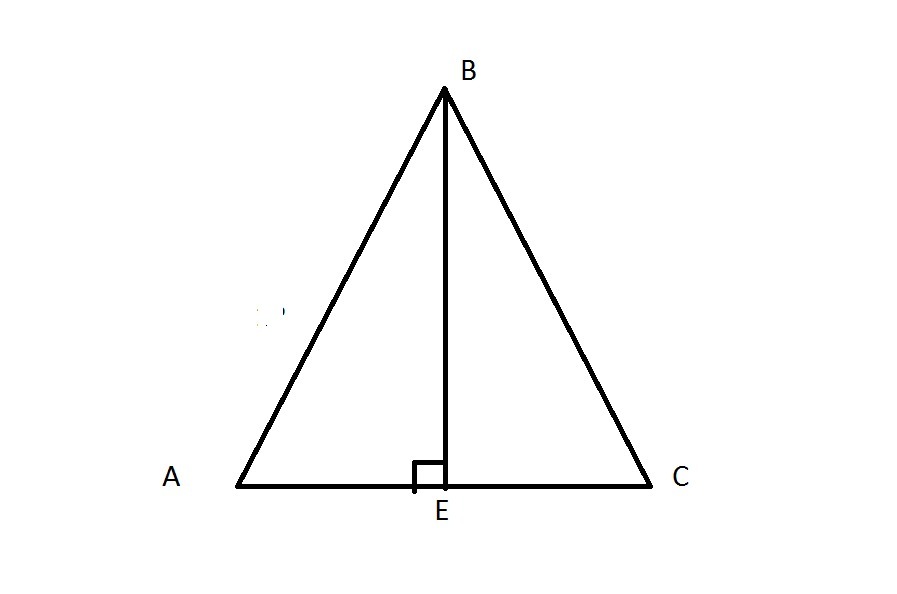
( Номер 1): в равнобедренном треугольнике АВС, ВЕ-высота, АВ=ВС. Найдите ВЕ, если АС=2 корня из 23 и АВ=12.
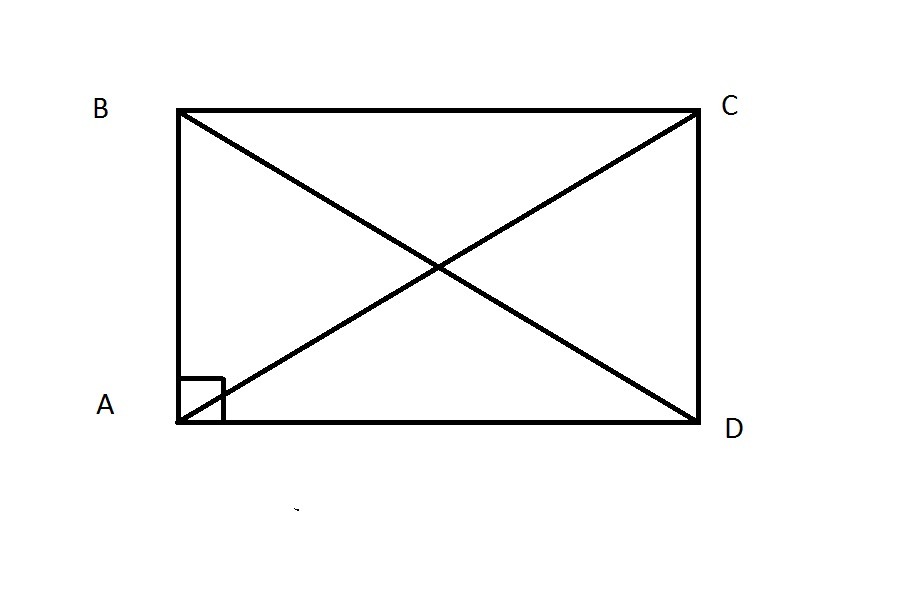
(Номер 2):В прямоугольном треугольнике АВСD найдите: ВD, если СD= корень из 0,63 и АD=0,9.
Ответы
Автор ответа:
0
Номер 1:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
⇒ AE=EC (т.к. BE - медиана)

ΔBEA - прямоугольный, т.к. BE - высота, а значит, ∠BEA=90°
По теореме Пифагора:

Номер 2.
Проводим диагональ AC, AC=BD как диагонали прямоугольника
 = 1,2
= 1,2
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
⇒ AE=EC (т.к. BE - медиана)
ΔBEA - прямоугольный, т.к. BE - высота, а значит, ∠BEA=90°
По теореме Пифагора:
Номер 2.
Проводим диагональ AC, AC=BD как диагонали прямоугольника
Приложения:
Похожие вопросы
Предмет: Биология,
автор: tonyaprudkaa
Предмет: Химия,
автор: kamillaknazeva50
Предмет: Обществознание,
автор: CblPKOCu4KA
Предмет: Физика,
автор: Аноним
Предмет: Литература,
автор: ganna7832