Предмет: Математика,
автор: NastyaLon
(x! + (x+2)!) / (x-1)!+(x+2)!
Решите, пожалуйста
Ответы
Автор ответа:
0
вот правильно:
(x! + (x+2)!) / (x-1)!+(x+2)!=x!+(x+2)(x+1)x!/(x-1)!+(x+2)(x+1)x(x-1)!=x!(1+(x+2)(x+1))/(x-1)!(1+(x+2)(x+1)x)=x(x-1)!(1+x²+x+2x+2)/(x-1)!(1+(x²+2x)(x+1))=x(3+x²+3x)/1+x³+x²+2x²+2x=3x+x³+3x²/1+x³+3x²+2x=x³+3x²+3x/x³+3x²+2x+1
(x! + (x+2)!) / (x-1)!+(x+2)!=x!+(x+2)(x+1)x!/(x-1)!+(x+2)(x+1)x(x-1)!=x!(1+(x+2)(x+1))/(x-1)!(1+(x+2)(x+1)x)=x(x-1)!(1+x²+x+2x+2)/(x-1)!(1+(x²+2x)(x+1))=x(3+x²+3x)/1+x³+x²+2x²+2x=3x+x³+3x²/1+x³+3x²+2x=x³+3x²+3x/x³+3x²+2x+1
Приложения:
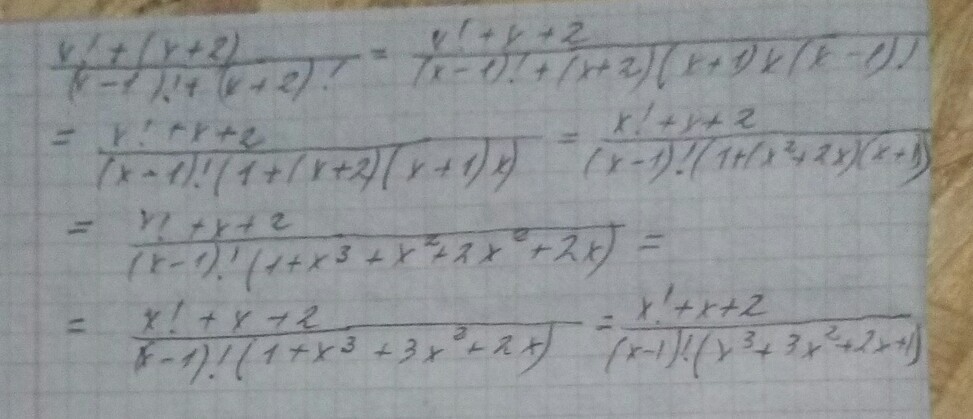
Автор ответа:
0
Просто ответ должен быть 1
Автор ответа:
0
проверь правильность записи примера, т.к. у меня там единицы не получилось
Автор ответа:
0
ну я как-бы ище проверила решения через онлайн калькулятор
Автор ответа:
0
в числителе примера не х!+ (х+2), а х!+(х+2)!
Похожие вопросы
Предмет: Химия,
автор: komila61008
Предмет: Русский язык,
автор: Аноним
Предмет: Физика,
автор: whereisme00
Предмет: География,
автор: Sonya200429
Предмет: Физика,
автор: нара10