Предмет: Алгебра,
автор: khalitovroman
Anonim know everything xD
2cos^2 t+sin t+1=0
sin^2 t+3cos t-3=0
Приложения:
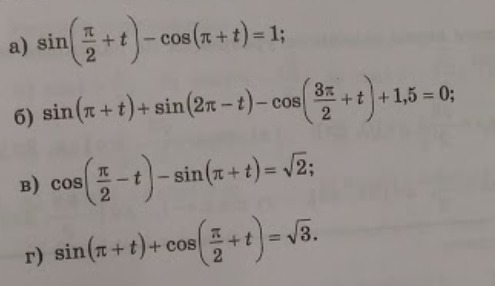
Ответы
Автор ответа:
0
Автор ответа:
0
https://znanija.com/task/27123041 final
Похожие вопросы
Предмет: Русский язык,
автор: drakonkrytoi
Предмет: Геометрия,
автор: newsgwt
Предмет: Другие предметы,
автор: maksamoshkin2010
Предмет: Математика,
автор: Alexander357951
Предмет: Математика,
автор: саша705