Предмет: Геометрия,
автор: Вишенка3095
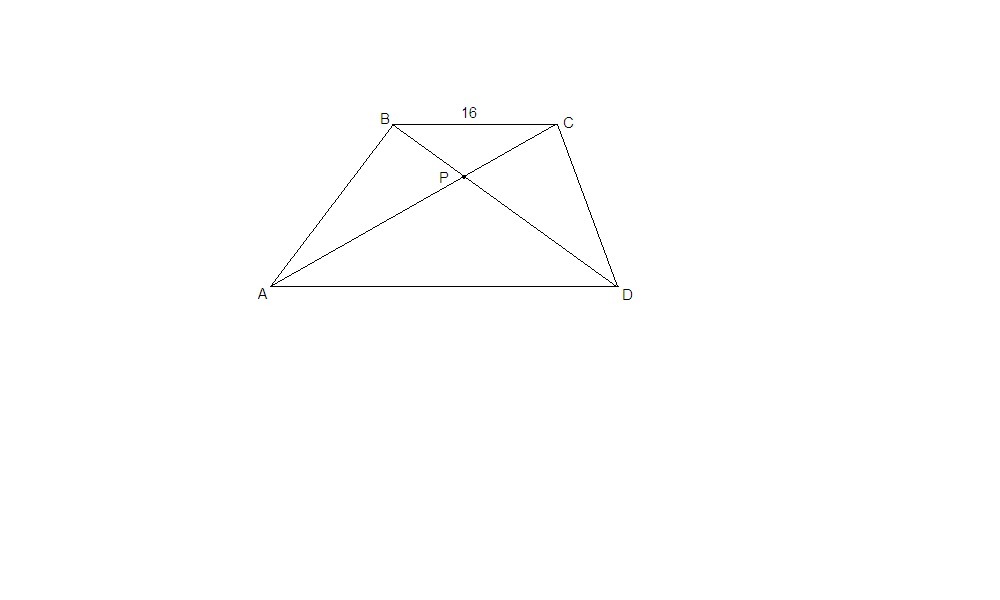
В трапеции ABCD ( AD||ВС) диагонали АС и BD пересекаюся в точке Р. а) Докажите, что треугольники АPD и СРВ подобны. б) Найдите основание AD трапеции ABCD, если известно, что АР : АС=7:9, ВС = 16.
Ответы
Автор ответа:
0
∠PAD = ∠PCB как накрест лежащие при пересечении параллельных прямых AD и ВС секущей АС,
∠ВРС = ∠DPA как вертикальные, значит
ΔCPB подобен ΔAPD по двум углам.
AP : AC = 7 : 9
Значит, АР составляет 7 равных частей, а РС - 2 таких части.
Из подобия треугольников:
АР : PC = AD : BC
7 : 2 = AD : 16
AD = 16 · 7 / 2 = 56
∠ВРС = ∠DPA как вертикальные, значит
ΔCPB подобен ΔAPD по двум углам.
AP : AC = 7 : 9
Значит, АР составляет 7 равных частей, а РС - 2 таких части.
Из подобия треугольников:
АР : PC = AD : BC
7 : 2 = AD : 16
AD = 16 · 7 / 2 = 56
Приложения:
Похожие вопросы