Предмет: Математика,
автор: Аноним
Сумма трех чисел образующих геометрическую прогрессию равна 39. Если первое число умножить на -3,то получиться арифметическая пргрессия. Найти 3 первоначальных числа
Ответы
Автор ответа:
0
Первое число x, второе xq, третье xq² (q - знаменатель прогрессии). Причём q>0.
По условию
x+xq+xq² = 39
x(q²+q+1) = 39 (1)
-3x, xq, xq² - арифметическая прогрессия. То есть
xq-(-3x) = xq²-xq
xq+3x = xq²-xq (2)
Составим и решим систему уравнений:

По условию
x+xq+xq² = 39
x(q²+q+1) = 39 (1)
-3x, xq, xq² - арифметическая прогрессия. То есть
xq-(-3x) = xq²-xq
xq+3x = xq²-xq (2)
Составим и решим систему уравнений:
Приложения:
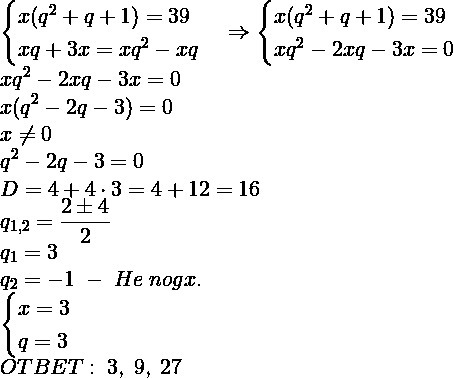
Похожие вопросы
Предмет: Английский язык,
автор: bogomol433
Предмет: История,
автор: peowownooz
Предмет: Литература,
автор: svetlanaorlioglo
Предмет: Информатика,
автор: ДашаВласоваИнна