Предмет: Геометрия,
автор: hdhdjdkjdjd172
Острый угол ромба равен 60°. Длина большей его диагонали -12√3см. Вычислете площадь ромба
Ответы
Автор ответа:
0
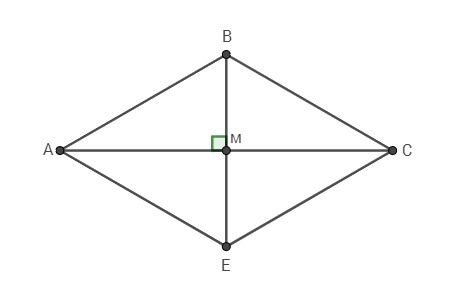
Пусть дан ромб АВСЕ
М - точка пересечения диагоналей
∠ВАЕ = 60°
АС = 12√3
Найти: S(АВСЕ)
Диагонали ромба пересекаются под прямым углом, в точке пересечения длятся пополам ⇒
АМ = АС/2 = (12√3)/2 = 6√3
Диагонали ромба являются биссектрисами его углов ⇒
∠ВАМ = ∠ВАЕ/2 = 60/2 = 30°
Из ΔАВМ:

BE = 2*BM = 2*6 = 12 cм
 см²
см²
Ответ: 72√3 см²
М - точка пересечения диагоналей
∠ВАЕ = 60°
АС = 12√3
Найти: S(АВСЕ)
Диагонали ромба пересекаются под прямым углом, в точке пересечения длятся пополам ⇒
АМ = АС/2 = (12√3)/2 = 6√3
Диагонали ромба являются биссектрисами его углов ⇒
∠ВАМ = ∠ВАЕ/2 = 60/2 = 30°
Из ΔАВМ:
BE = 2*BM = 2*6 = 12 cм
Ответ: 72√3 см²
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: anzelikkaaa
Предмет: Математика,
автор: selfi1337228
Предмет: Геометрия,
автор: islamtigerr
Предмет: Алгебра,
автор: arzuaskerova2
Предмет: Математика,
автор: кристина547