Предмет: Математика,
автор: natali2609
Помогите пожалуйста решить!
дифференцированное уравнение кто умеет и может!
Приложения:
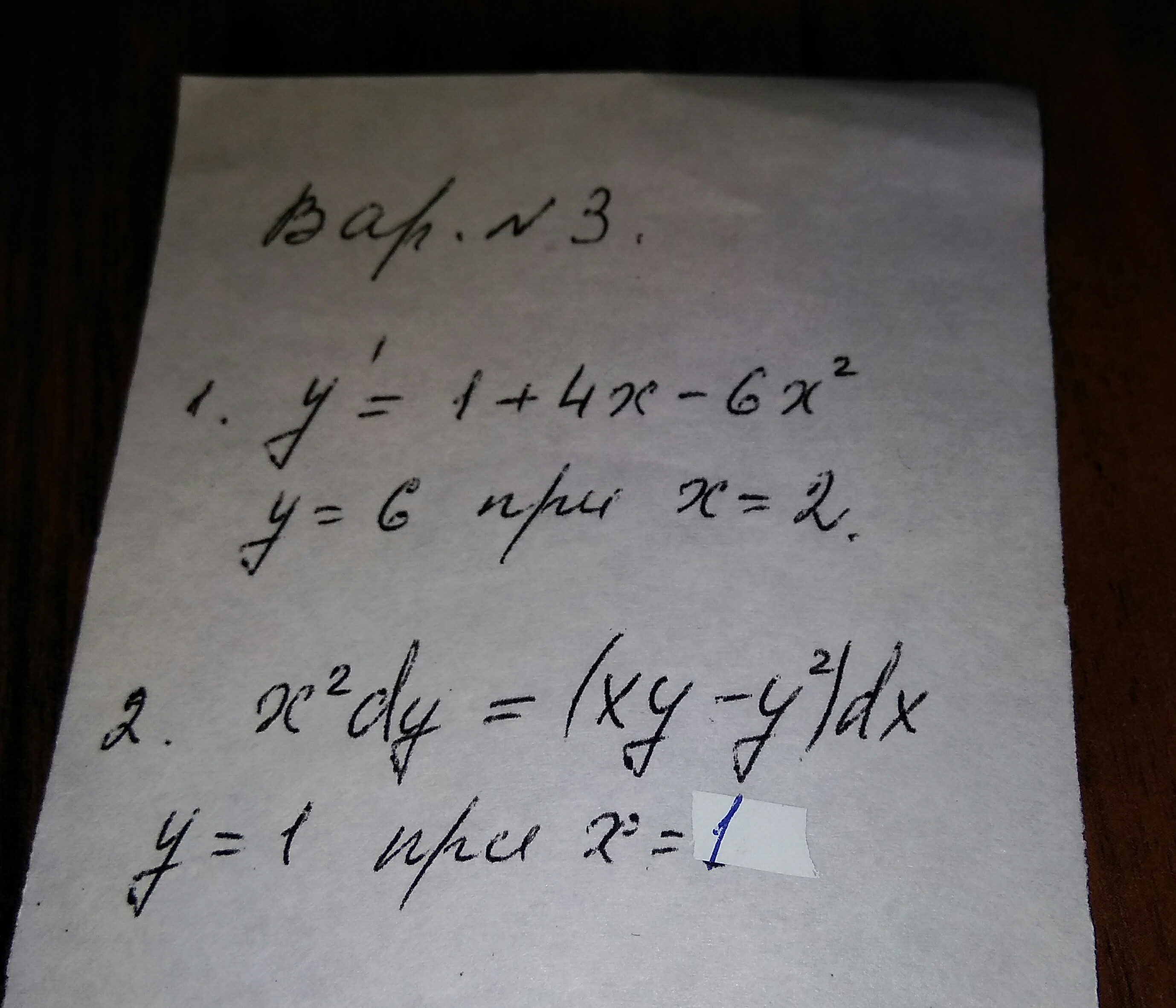
Ответы
Автор ответа:
0
1. Интегрируя левую и правую части уравнения, получим

Получили это общее решение ДУ. Осталось найти частное решение, подставив начальные условия.

 частное решение
частное решение
2. Переписав данное ДУ в следующем виде . И этот вид ДУ является однородным(выполняется условие однородности).
. И этот вид ДУ является однородным(выполняется условие однородности).
Пусть тогда по правилу дифференцирования произведения двух функций :
тогда по правилу дифференцирования произведения двух функций : 

И это последнее уравнение является ДУ с разделяющимися переменными

тогда, осуществив замену , получим
, получим 
Подставляя начальные условия, получим частное решение:

 - частное решение.
- частное решение.
Получили это общее решение ДУ. Осталось найти частное решение, подставив начальные условия.
2. Переписав данное ДУ в следующем виде
Пусть
И это последнее уравнение является ДУ с разделяющимися переменными
тогда, осуществив замену
Подставляя начальные условия, получим частное решение:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: makpalkanatkyzy06
Предмет: Математика,
автор: plotnikovdaniil63
Предмет: Химия,
автор: Аноним
Предмет: Алгебра,
автор: Лристина3000
Предмет: Биология,
автор: taisiapavlova