Question

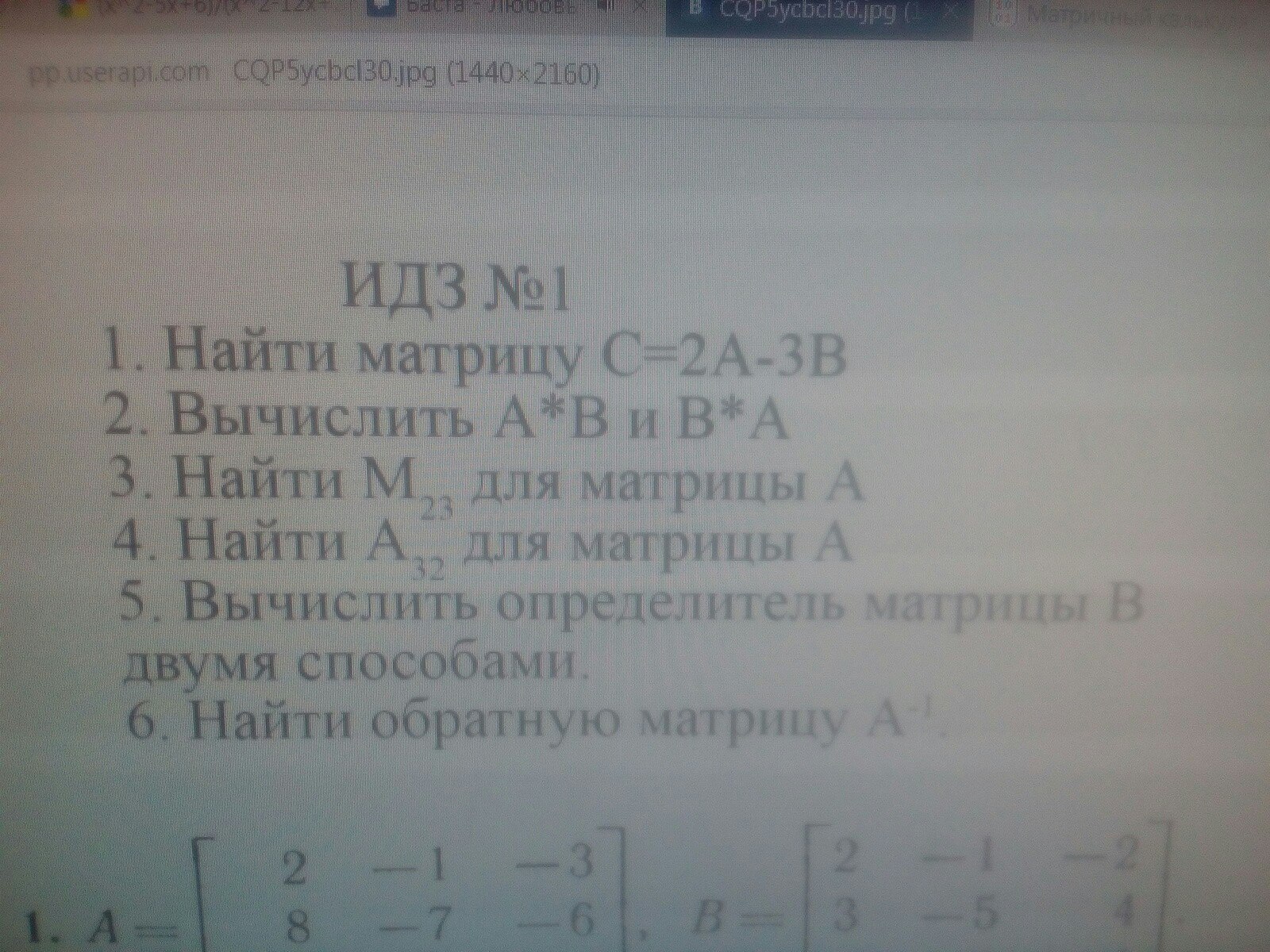
Помогите решить пожалуйста, завтра в 9 00 зачет. Матрица.

Answer 1

1)
$C=2A-3B= left[begin{array}{ccc}4&4&10\6&6&12\8&6&8end{array}right] - left[begin{array}{ccc}3&-3&3\6&9&9\3&-6&-3end{array}right] = left[begin{array}{ccc}1&7&7\0&-3&3\5&12&11end{array}right]$

2)
$A*B= left[begin{array}{ccc}2&2&5\3&3&6\4&3&4end{array}right] * left[begin{array}{ccc}1&-1&1\2&3&3\1&-2&-1end{array}right] = \ = left[begin{array}{ccc}2+4+5&-2+6-10&2+6-5\3+6+6&-3+9-12&3+9-6\4+6+4&-4+9-8&4+9-4end{array}right] = left[begin{array}{ccc}11&-6&3\15&-6&6\14&-3&9end{array}right]$

$B*A=left[begin{array}{ccc}1&-1&1\2&3&3\1&-2&-1end{array}right]*left[begin{array}{ccc}2&2&5\3&3&6\4&3&4end{array}right]= left[begin{array}{ccc}3&2&3\25&22&40\-8&-7&-11end{array}right]$

3) $M_{23}= left|begin{array}{cc}2&2\4&3end{array}right|= 2*3-4*2=6-8=-2$

4) $A_{32}=(-1)^{3+2}*left|begin{array}{cc}2&5\3&6end{array}right|=-(2*6-3*5)= -(12-15)=3$

5) Определитель |B| способом треугольника
$|B|= left|begin{array}{ccc}1&-1&1\2&3&3\1&-2&-1end{array}right|=1*3(-1)+1*3(-1)+1*2(-2)- \ -1*3*1-2(-1)(-1)-1*3(-2) =-3-3-4-3-2+6=-9$

Определитель |B| способом разложения по строке
$|B|= left|begin{array}{ccc}1&-1&1\2&3&3\1&-2&-1end{array}right|=1*left|begin{array}{cc}3&3\-2&-1end{array}right|+1*left|begin{array}{cc}2&3\1&-1end{array}right|+ \ +1*left|begin{array}{cc}2&3\1&-2end{array}right|=-3+6-2-3-4-3=-9$

6) Обратная матрица $A^{-1}$
а) Определитель |A|
$|A|= left|begin{array}{ccc}2&2&5\3&3&6\4&3&4end{array}right| =2*3*4+3*3*5+2*6*4-4*3*5- \ -3*2*4-3*6*2=24+45+48-60-24-36=-3$

б) Матрица алгебраических дополнений
$A_{11}=(-1)^{1+1}*left|begin{array}{cc}3&6\3&4end{array}right|=12-18=-6$
$A_{12}=(-1)^{1+2}*left|begin{array}{cc}3&6\4&4end{array}right|=-(12-24)=12$
$A_{13}=(-1)^{1+3}*left|begin{array}{cc}3&3\4&3end{array}right|=9-12=-3$
$A_{21}=(-1)^{2+1}*left|begin{array}{cc}2&5\3&4end{array}right|=-(8-15)=7$
$A_{22}=(-1)^{2+2}*left|begin{array}{cc}2&5\4&4end{array}right|=8-20=-12$
$A_{23}=(-1)^{2+3}*left|begin{array}{cc}2&2\4&3end{array}right|=-(6-8)=2$
$A_{31}=(-1)^{3+1}*left|begin{array}{cc}2&5\3&6end{array}right|=12-15=-3$
$A_{32}=(-1)^{3+2}*left|begin{array}{cc}2&5\3&6end{array}right|=-(12-15)=3$
$A_{33}=(-1)^{3+3}*left|begin{array}{cc}2&2\3&3end{array}right|=6-6=0$

в) Транспонированная матрица алгебраических дополнений:
$A^T= left[begin{array}{ccc}-6&7&-3\12&-12&3\-3&2&0end{array}right]$

г) Обратная матрица - это транспонированная матрица дополнений, деленная на определитель исходной матрицы.
$A{-1}= left[begin{array}{ccc}2&-7/3&1\-4&4&-1\1&-2/3&0end{array}right]$

ВСЁ!

Answer 2

Офигеть.. Спасибо вам, честно, не ожидал что так чётко напишите. Благодарю

Answer 3

Пожалуйста