Question

Комплексные числа вычислить
(-1-i)^1/5

Answer 1

Рассмотрим $z=-1-i$. Модуль комплексного числа: $|z|= sqrt{(-1)^2+(-1)^2} = sqrt{2}$

Тогда

                    $z=-1-i=sqrt{2}cdot bigg(- dfrac{1}{ sqrt{2} } - dfrac{i}{sqrt{2}}bigg)=sqrt{2}bigg(cos dfrac{5 pi }{4} +isin dfrac{5 pi }{4} bigg)$

Согласно формуле Муавра:

      $sqrt[5]{z}=sqrt[10]{2}bigg(cos dfrac{frac{5 pi }{4}+2 pi k}{5} +isin dfrac{frac{5 pi }{4}+2 pi k}{5} bigg)$, где k=0,...4

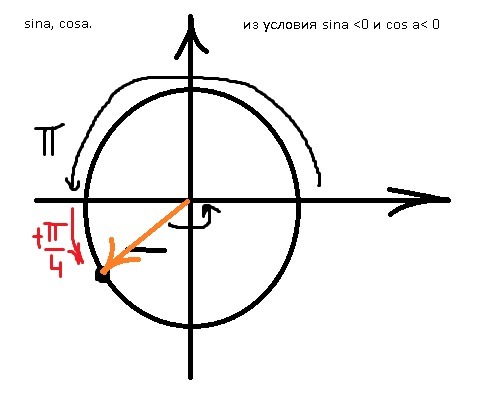
Дополнительное объяснение. Косинус отрицателен только в II и III четвертях, а синус - в III и IV. В нашем случае оба тригонометрические функции отрицательные, т.е. синус и косинус будут отрицательны только в III четвертях.(нахождение угла смотрите во вложении картинки)

Answer 2

а формула Муавра одна, а эта как я помню называется аналогичная формуле Муавра из ненулевого комлексного числа

Answer 3

arg z = arctg (-1)/(-1) +pi = pi/4 + pi = 5pi/4

Answer 4

Это формулой можно воспользоваться, если угол не так уж и точный

Answer 5

Но я предпочитаю на окружности :)

Answer 6

Спасибо за сотрудничество !