Question

Помогите решить пожалуйста.

Answer 1

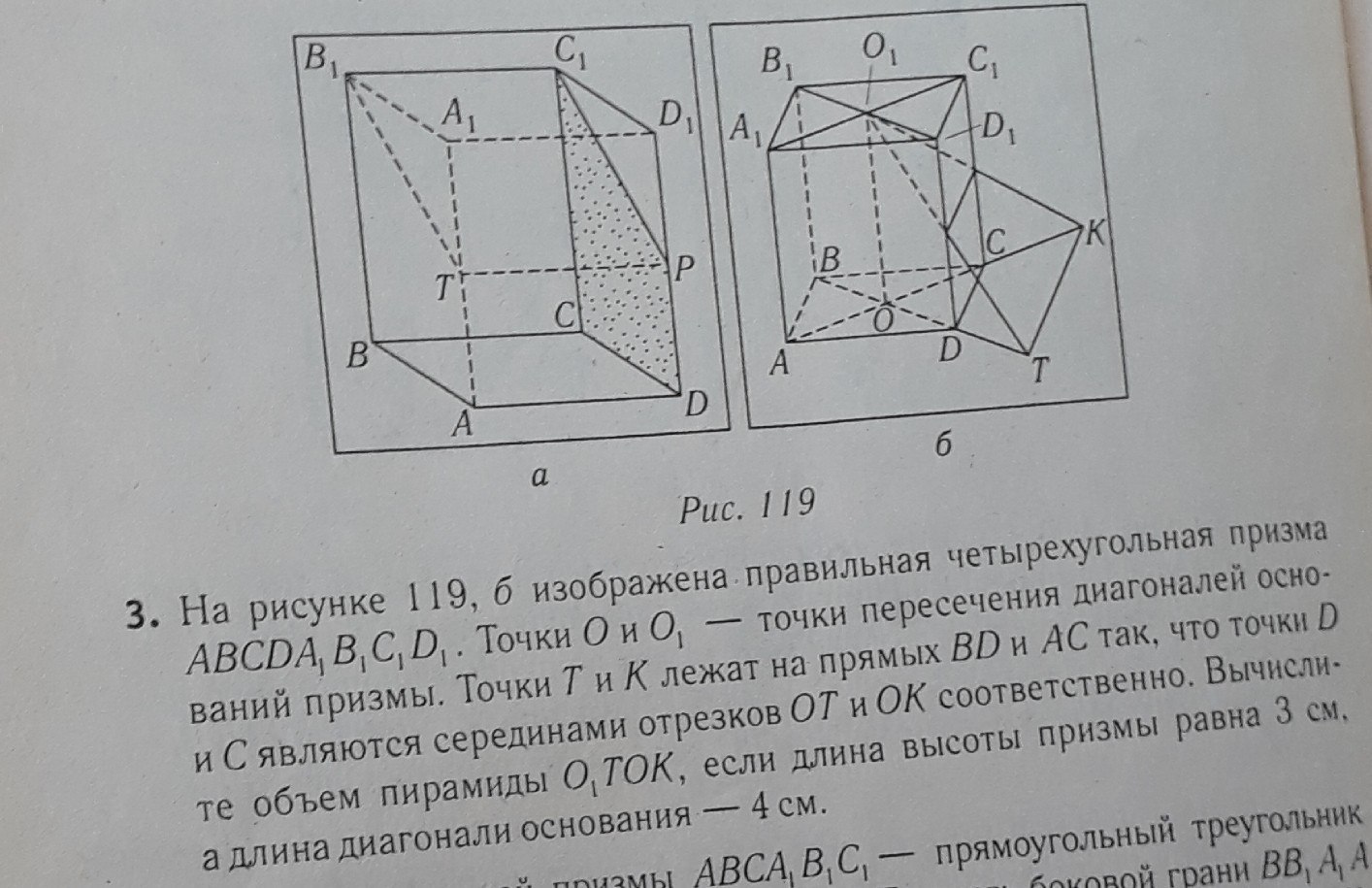
Задание 3 с рисунком 119 б.

На основе задания определяем, что отрезки ОТ и ОК равны диагоналям основания исходной призмы, то есть по 4 см.
Угол между ОТ и ОК равен 90 градусов как между диагоналями квадрата в основании исходной призмы.
Треугольник ОКТ - прямоугольный, его площадь So = (1/2)*4*4 = 8 см².
Тогда объём заданной пирамиды равен:
V = (1/3)So*H =(1/3)*8*3 = 8 см³.