Предмет: Алгебра,
автор: Юленька194
логарифмическое неравенство. я решила, но меня смущает ответ. хочу свериться
Приложения:
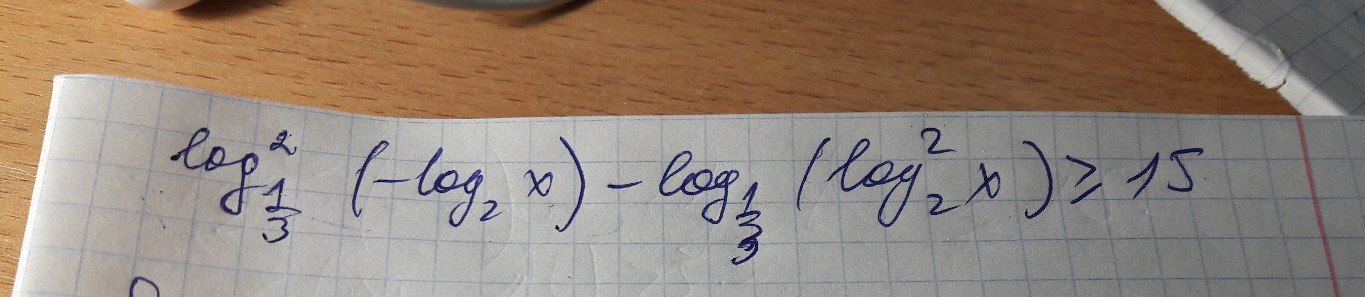
Ответы
Автор ответа:
0
Приложения:

Похожие вопросы
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: katamoguceva1
Предмет: Математика,
автор: snezanaomg2069
Предмет: Биология,
автор: katya29032002
Предмет: Биология,
автор: vislobokova200