Тест 9.Площадь трапеции. Вариант 1

Ответы
Вариант 1
А1:
Площадь трапеции вычисляется по формуле:
S = (a+b)•h/2 , где а и b - основания трапеции, h - высота трапеции
Подставим известные данные и находим ответ:
S = (5 + 9)•6/2 = 14•3 = 42 см²
ОТВЕТ: 3
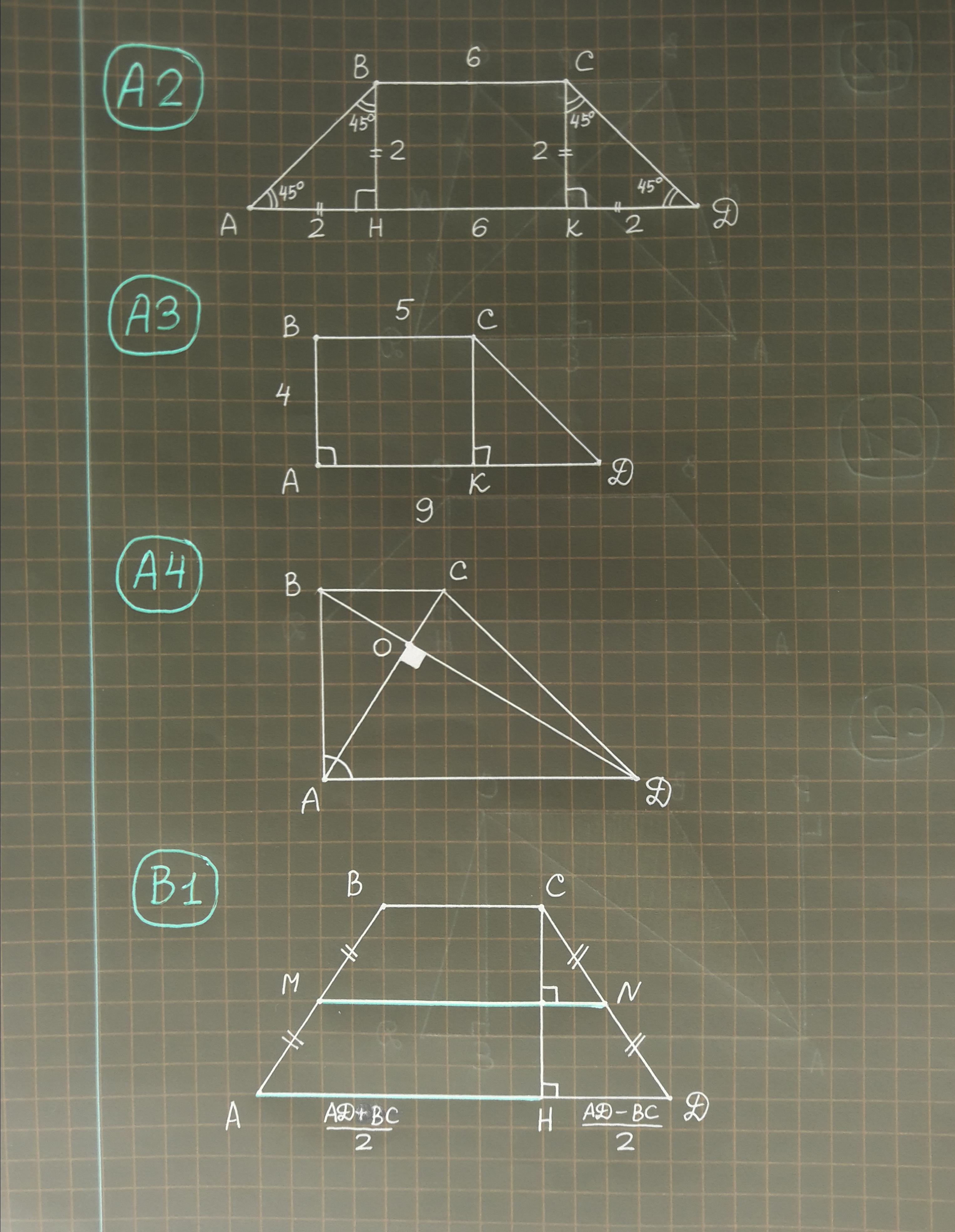
А2:
Высоты ВН и СК делят равнобокую трапецию АВСD на прямоугольник и два равных прямоугольных равнобедренных треугольника (угол при основании трапеции 45°) ⇒ BC = HK = 6 см ,
АН = ВН = СК = KD = (AD - HK)/2 = (10 - 6)/2 = 2 см
S abcd = (BC + AD)•BH/2 = (6 + 10)•2/2 = 16 см²
ОТВЕТ: 1
A3:
В прямоугольной трапеции АВCD (∠A = 90°) опустим высоту СК ⇒ АВ = СК . В ΔСКD (∠CKD = 90°): как известно, в прям-ом тр-ке гипотенуза всегда больше катетов, CK < CD ⇒ AB < CD , AB = 4 см - меньшая боковая сторона трапеции
S abcd = (BC + AD)•AB/2 = (5 + 9)•4/2 = 14•2 = 28 см²
ОТВЕТ: 4
А4:
Если в четырёхугольнике диагонали взаимно перпендикулярны, то его площадь равна половине произведения его диагоналей
S abcd = AC•BD/2 = 12•18/2 = 12•9 = 108 см²
ОТВЕТ: 1
В1:
В равнобокой трапеции высота, опущенная на бОльшее основание, делит его на два отрезка, бОльший из которых равен полусумме оснований, а мЕньший - полуразности оснований. Больший отрезок равен полусумме оснований - это по определению средняя линия данной трапеции.
Площадь трапеции можно вычислять и по-другому: она равна произведению средней линии трапеции на высоту ИЛИ произведению бОльшего отрезка, которого высота трапеции делит бОльшее основание, на саму высоту
S abcd = (BC + AD)•CH/2 = MN•CH = AH•CH = 26•10 = 260 см²
ОТВЕТ: 260 см²
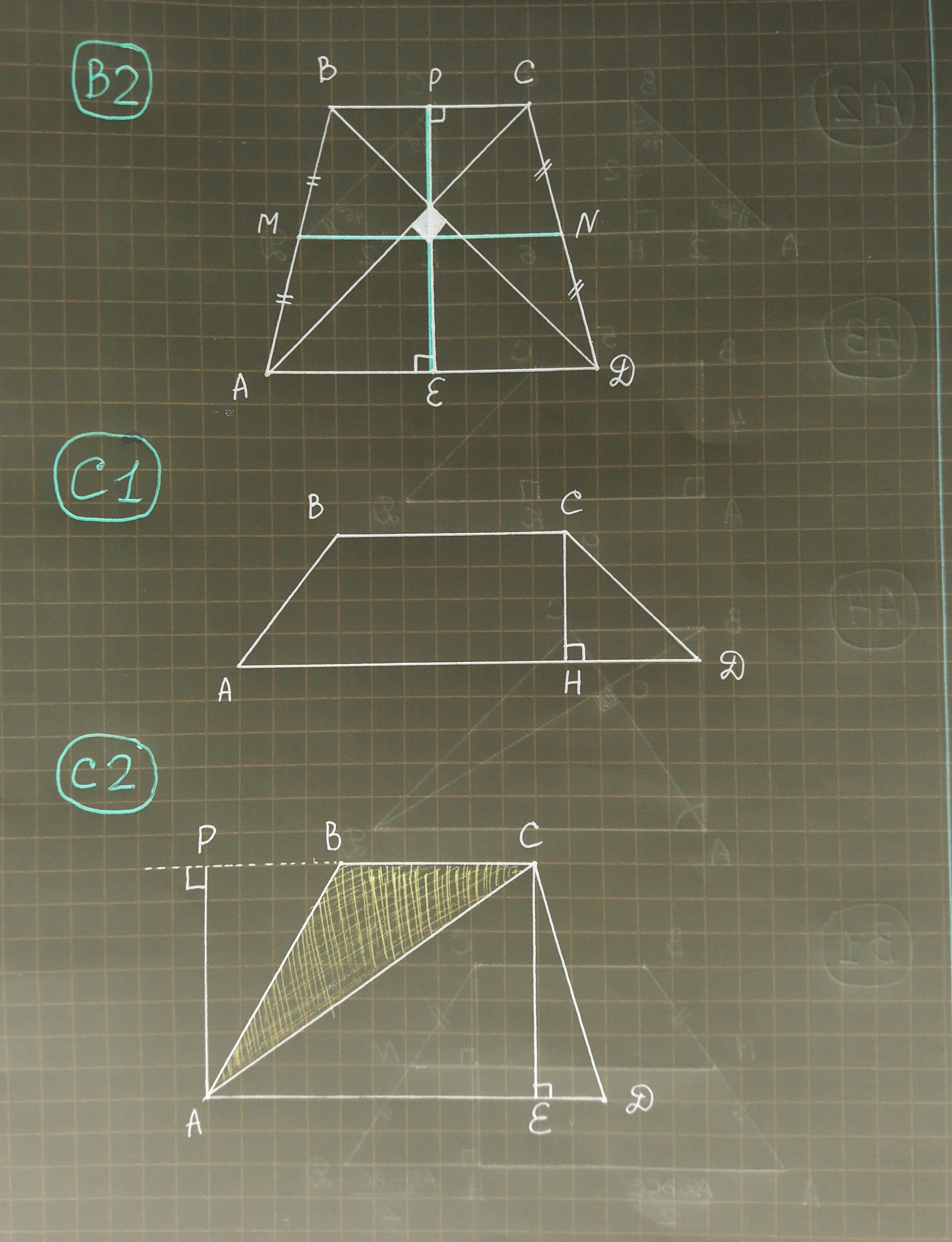
В2:
Если в РАВНОБОКОЙ трапеции диагонали взаимно перпендикулярны, то его высота равна средней линии трапеции ⇒ PE = MN
S abcd = (BC + AD)•PE/2 = MN•PE = PE² = 18² = 324 см²
ОТВЕТ: 324 см²
C1:
Если высота меньше оснований и присутствуют отношения, то пусть СН = 4х, ВС = 5х, АD = 6x, тогда составим уравнение:
S abcd = (BC + AD)•CH/2 = (5x + 6x)•4x/2 = 88 см²
11х•2х = 88 ⇔ 22х² = 88 ⇔ х² = 4 ⇔ х = 2
Значит, CH = 4x = 4•2 = 8 см, AD = 6x = 6•2 = 12 см
ВС = 5х = 5•2 = 10 см - меньшее основание трапеции
ОТВЕТ: 10 см
С2:
Полное условие:
В трапеции ABCD BC и AD - основания, BC : AD = 3 : 4. Площадь трапеции равна 70 см². Найдите площадь треугольника АВС.
ΔАВС и ΔACD имеют равные высоты АР и СЕ
Если два треугольника имеют равные высоты или они совпадают, то их площади относятся как основания, к которым проведены высоты
S abc / S acd = BC/AD = 3/4
Значит, S abc = (3/7) • S abcd = (3/7) • 70 = 3•10 = 30 см²
ОТВЕТ: 30 см²