Предмет: Геометрия, автор: polisa21

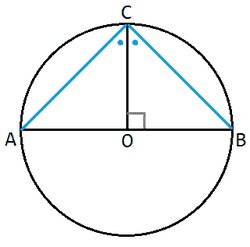
В окружности с центром О проведён диаметр АВ и перпендикулярный ему радиус ОС. Докажите, что ОС-биссектриса угла АСВ
(желательно с рисунком)

Ответы

Автор ответа: siestarjoki

0

OA=OB=OC (радиусы)
∠AOC=∠BOC=90 (OC⊥AB)
△AOC=△BOC (по двум сторонам и углу между ними)
∠ACO=∠BCO, OC - биссектриса ∠ACB

Приложения:

Предыдущий вопрос

Следующий вопрос

Похожие вопросы

Предмет: Информатика, автор: alina9316

Егор придумал новый шифр, основанный на вращении кубика. Суть этого шифра проста: вы берете кубик, на каждой грани которого краской нарисована какая-то буква, затем ставите его на ровную поверхность. После этого необходимо начать перекатывать кубик через ребро в соответствии со строкой-ключом: F — вперед от вас, B — назад к вам, L — влево, R — вправо. Каждый раз, когда кубик касается своей нижней гранью поверхности, он оставляет на ней след. После перекатываний кубика на поверхности отпечатываются буквы, которые образуют загаданное слово (из букв в том порядке, в котором были оставлены отпечатки). Егор зашифровал слово, а после этого, к сожалению, забыл его. У него есть развертка кубика, а также строка-ключ, в соответствии с которой шифровали слово. Помогите Егору восстановить загаданное слово. На рисунке слева представлена развертка, а справа — вид куба сзади справа. При этом буква «A» находится на верхней грани, «T» — на правой, «N» — на левой, «E» — на нижней. Грань с буквой «H» смотрит на вас, а грань с буквой «R» находится напротив нее. Обратите внимание, что кубик уже стоит на букве «E», поэтому она сразу же отпечатается на поверхности. Вы видите только букву «H», причем на правой грани расположена буква «T», а на верхней — «A». Строка-ключ для кубика выглядит следующим образом: «RBLLBRR» Ответом на данную задачу является исходное слово, записанное заглавными английскими буквами

6 лет назад

Предмет: Алгебра, автор: UUU888

срочно срочно срочно

6 лет назад

Предмет: География, автор: mariaromanova127

причини вулканічної активності у регіоні Індонезії

6 лет назад

Предмет: Алгебра, автор: bloshaket

6-x/5+x/4=1 решите пожалуйста уравнение

10 лет назад

Предмет: Математика, автор: snega145145Jimkerri

Решите уравнение.
3x-916=x+240.

10 лет назад