Предмет: Алгебра,
автор: kuzya40456
Подробное решение .очень срочно требуется!
Приложения:
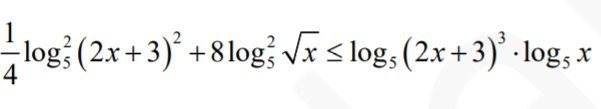
Ответы
Автор ответа:
0
ОДЗ: {2x + 3 > 0 => x > -1.5, x > 0, x >= 0} => x > 0.



Пусть log5(2x+3) = a, log5(x) = b, тогда уравнение примет вид:
a^2 + 2b^2 <= 3ab
(a-b)^2 + b^2 - ab <= 0
(a-b)^2 <= ab - b^2
(a-b)^2 <= b(a - b)
Т. к. a - b > 0 на ОДЗ, поделим обе части неравенства на (a - b) и получим:
a-b <= b
a <= 2b
Вернемся к x:
log5(2x+3) <= 2log5(x)
log5(2x+3) <= log5(x*x)
2x + 3 <= x^2
x^2 - 2x - 3 >= 0
x1 = -1, x2 = 3
Неравенство справедливо на участке x E (-бесконечность; -1] U [3; бесконечность).
С учетом ОДЗ (x > 0) имеем x E [3; бесконечность).
Ответ: x E [3; бесконечность).
Пусть log5(2x+3) = a, log5(x) = b, тогда уравнение примет вид:
a^2 + 2b^2 <= 3ab
(a-b)^2 + b^2 - ab <= 0
(a-b)^2 <= ab - b^2
(a-b)^2 <= b(a - b)
Т. к. a - b > 0 на ОДЗ, поделим обе части неравенства на (a - b) и получим:
a-b <= b
a <= 2b
Вернемся к x:
log5(2x+3) <= 2log5(x)
log5(2x+3) <= log5(x*x)
2x + 3 <= x^2
x^2 - 2x - 3 >= 0
x1 = -1, x2 = 3
Неравенство справедливо на участке x E (-бесконечность; -1] U [3; бесконечность).
С учетом ОДЗ (x > 0) имеем x E [3; бесконечность).
Ответ: x E [3; бесконечность).
Похожие вопросы
Предмет: Қазақ тiлi,
автор: rebekkavilson
Предмет: Русский язык,
автор: Аноним
Предмет: Литература,
автор: angelinaborozdina092
Предмет: Математика,
автор: сардор12
Предмет: Алгебра,
автор: Аноним