Предмет: Алгебра,
автор: HalkWhite
Решите пж!!! АЛГЕБРА!!!
Приложения:
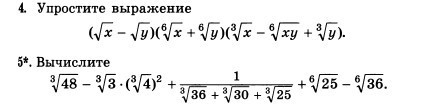
Ответы
Автор ответа:
0
-----------------------------------------------
Автор ответа:
0
кХМММ
Автор ответа:
0
Как это расшифруется?
Похожие вопросы
Предмет: Английский язык,
автор: nazgumassipova
Предмет: Математика,
автор: 13663212
Предмет: Обществознание,
автор: xhammd
Предмет: Математика,
автор: gulistan75
Предмет: Литература,
автор: zaia3