Предмет: Алгебра,
автор: david80
Найдите область определения функции:
Приложения:
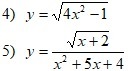
Ответы
Автор ответа:
0
4) Имеем корень, про него точно знаем, что подкоренное выражение должно быть не отрицательно.
в выражении имеем
имеем  . Очевидно, что равно
. Очевидно, что равно  выражение при
выражение при  и
и  . Разобьем как разность квадратов и решим методом интервалов
. Разобьем как разность квадратов и решим методом интервалов  . Отсюда
. Отсюда 
5) здесь в числителе корень и что делать уже знаем, в знаменателе квадратное уравнение и оно не должно равняться нулю, т.к. делить на нуль нельзя.
Делаем:

Я решу через т.Виетта, вы можете честно посчитать дискриминант и корни.

Итого получаем

в выражении
5) здесь в числителе корень и что делать уже знаем, в знаменателе квадратное уравнение и оно не должно равняться нулю, т.к. делить на нуль нельзя.
Делаем:
Я решу через т.Виетта, вы можете честно посчитать дискриминант и корни.
Итого получаем
Похожие вопросы
Предмет: Математика,
автор: aratunyan09
Предмет: Математика,
автор: karakulovalibek721
Предмет: Қазақ тiлi,
автор: ageng225
Предмет: Литература,
автор: Egor5423
Предмет: Алгебра,
автор: Эсфер