Предмет: Алгебра,
автор: Лерка009
Решите уравнение cos(pi/2+t)-sin(pi-t)=1
Ответы
Автор ответа:
0
Ответ:
Автор ответа:
0
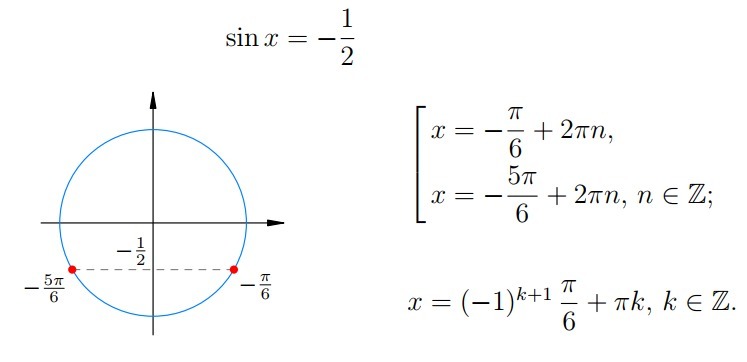
Приложения:
Похожие вопросы
Предмет: Қазақ тiлi,
автор: snipertyishrolbox11
Предмет: Литература,
автор: vladiktopik99
Предмет: Физика,
автор: dianaargunova228
Предмет: Математика,
автор: Evgenia137