Question

помогите решить!
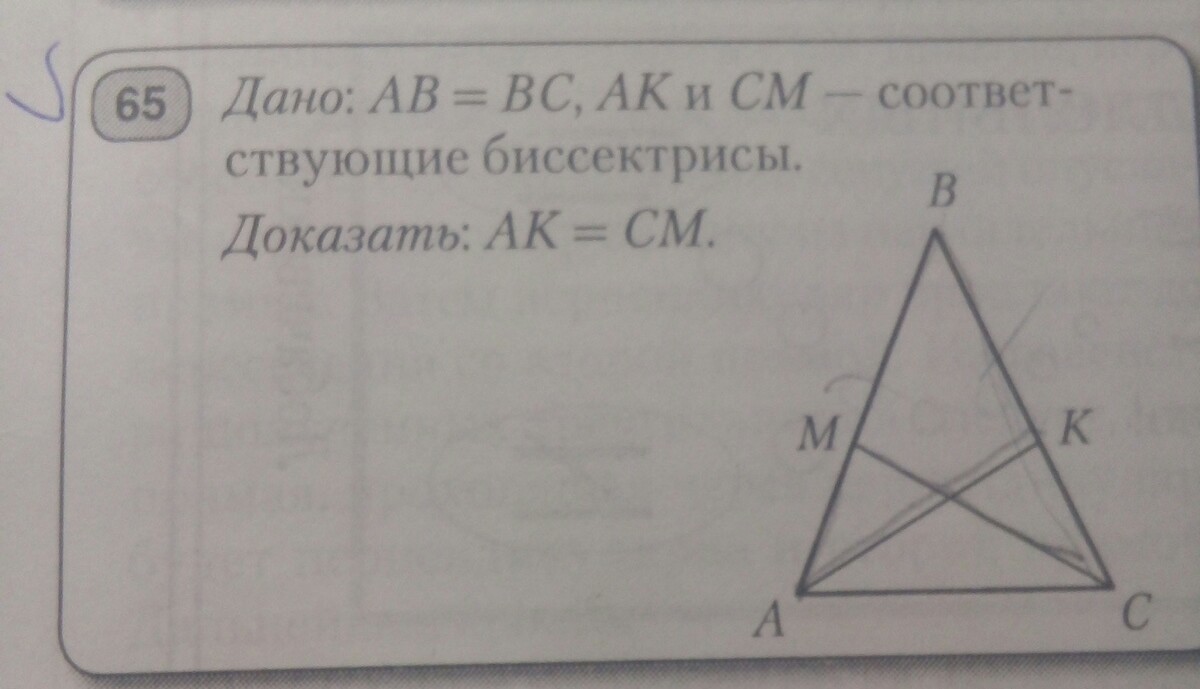
Дано: AB=BC, AK и CM- соответствующие биссектрисы.
Доказать: AK=CM.
Доказательство:
????????

Answer 1

Доказательство:  АК = СМ, т. к. в равнобедренном тр-ке биссектрисы, проведенные к боковым сторонам равны (по теореме);

Четырехугольник АМКС, где СМ и АК - диагонали, Δ АОС равнобедренный , <ОАС = <МАО = <АСО = <КСО = х; 
<АОС = <МОС = 180 - х - х = 180 - 2х. 
ΔМОК - равнобедренный.
Т.к. АК = МС и АО = ОС , то ОМ = ОК, <ОМК = <ОКМ = (180 - <МОК)/2 = 180 - (180 - 2х)/2 = х, т.е  <ОМК = <АСО и <ОАС = <ОКМ.

Если при пересечении двух прямых третьей внутренние разносторонние углы равны, то прямые параллельны (признаки параллельности прямых