Question

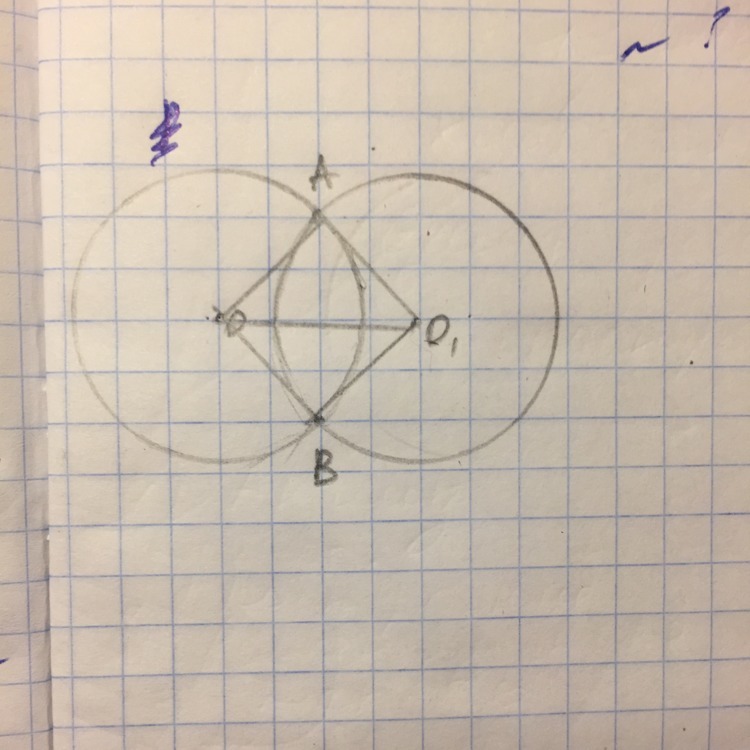
Две окружности с центрами O и O1 пересекаются в точках А и В. Докажите, что треугольники OAO1 и OBO1 равны.

Answer 1

Рассмотрим треугольники ОАО₁ и ОВО₁:

ОА = ОВ (радиусы окружности с центром О)
О₁А = О₁В (радиусы окружности с центром О₁)
ОО₁ - общая сторона

Следовательно, ΔОАО₁ = ΔОВО₁ по трем сторонам, что и требовалось доказать.

Answer 2

Спасибо))

Answer 3

пожалуйста