Предмет: Алгебра,
автор: panikvidze
Логарифмы. Задание на фото. Пожалуйста, с подробным решением.
Приложения:
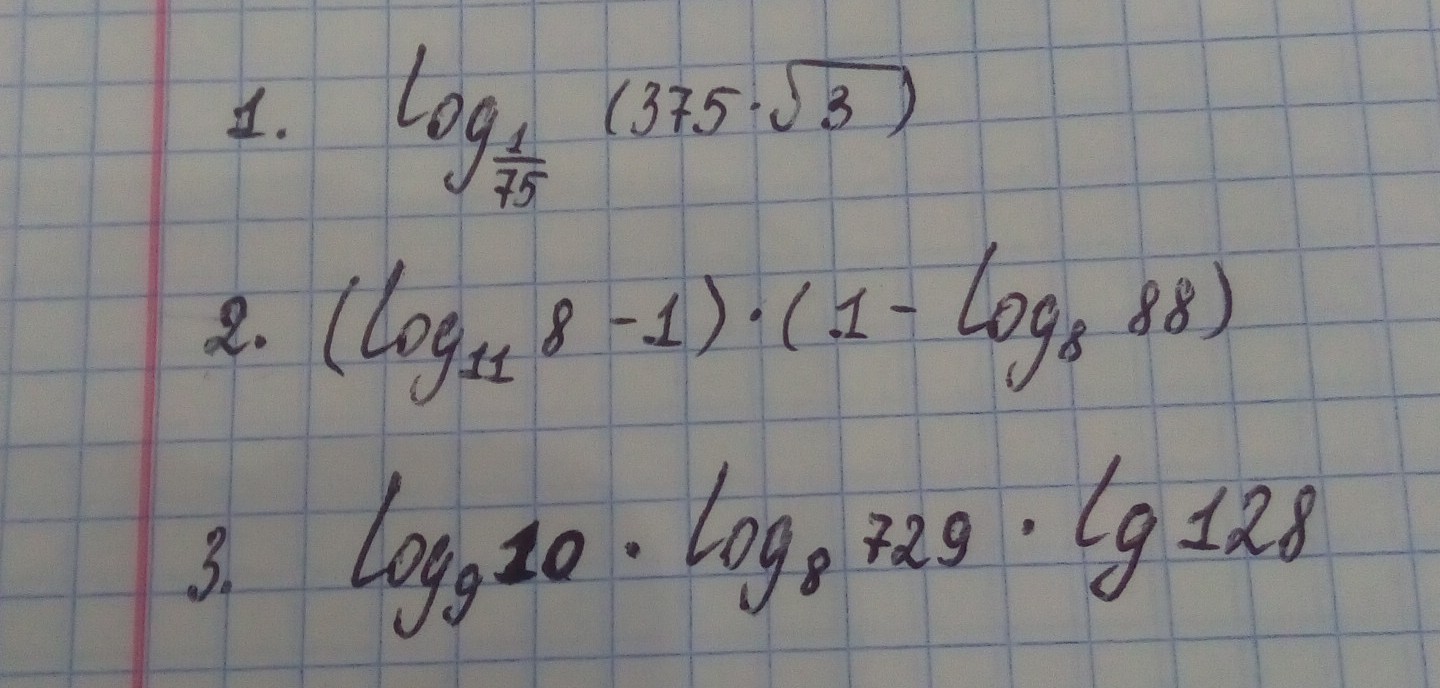
Ответы
Автор ответа:
1
если что-то непонятно спрашивай
Приложения:
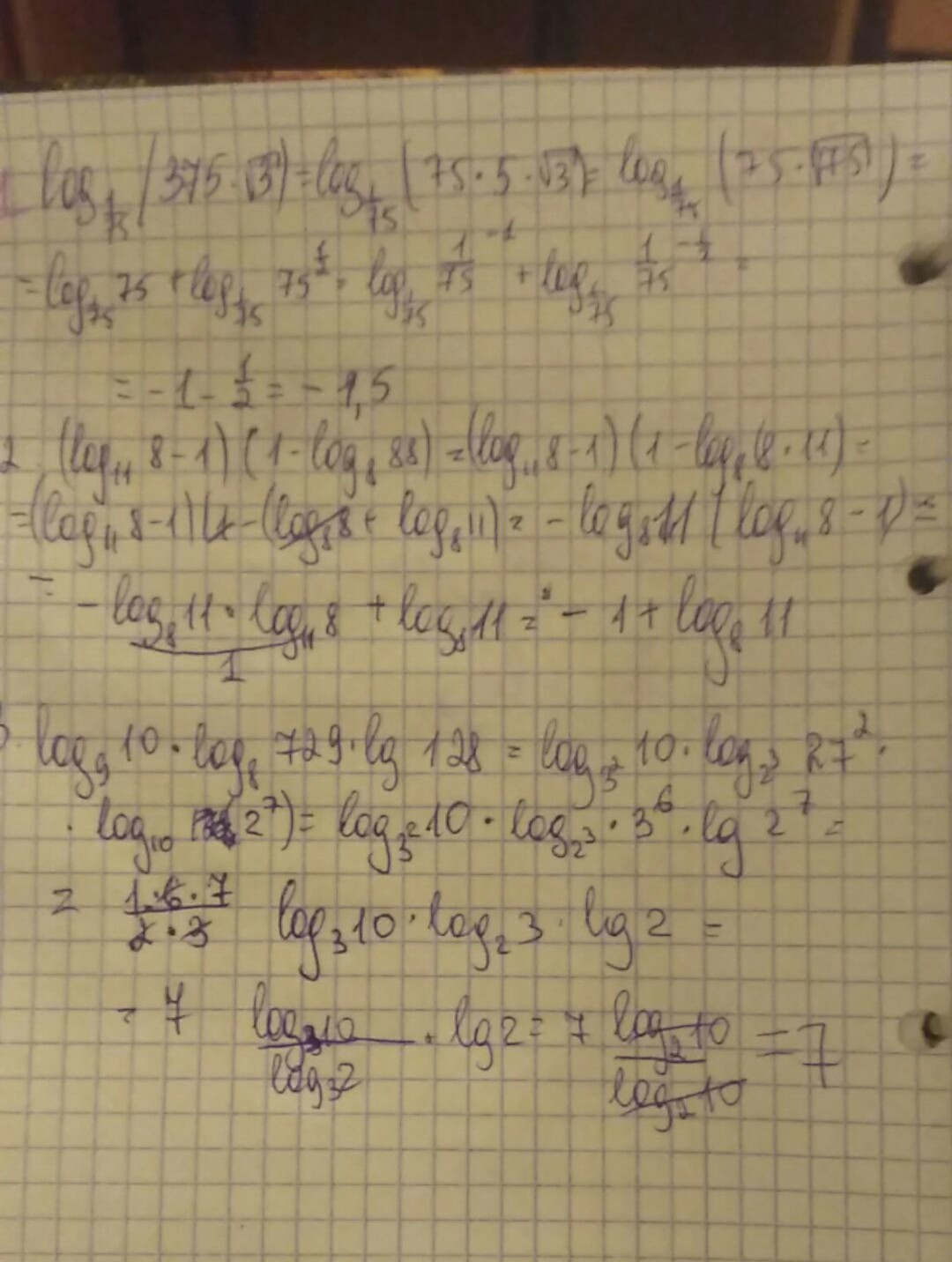
Автор ответа:
0
1. ![log_{frac{1}{75}}(375 sqrt{3} )=log_{75^{-1}}}(75*5 sqrt{3} )= frac{1}{-1}*log_{75}}(75* sqrt{3*5^2} )= \
=-log_{75}(75* sqrt{75} )=-[log_{75}(75)+log_{75}(75^ frac{1}{2} )]=\
=-[1+ frac{1}{2}*log_{75}(75) ]=-(1+ frac{1}{2} )=- frac{3}{2} log_{frac{1}{75}}(375 sqrt{3} )=log_{75^{-1}}}(75*5 sqrt{3} )= frac{1}{-1}*log_{75}}(75* sqrt{3*5^2} )= \
=-log_{75}(75* sqrt{75} )=-[log_{75}(75)+log_{75}(75^ frac{1}{2} )]=\
=-[1+ frac{1}{2}*log_{75}(75) ]=-(1+ frac{1}{2} )=- frac{3}{2}](https://tex.z-dn.net/?f=log_%7Bfrac%7B1%7D%7B75%7D%7D%28375+sqrt%7B3%7D+%29%3Dlog_%7B75%5E%7B-1%7D%7D%7D%2875%2A5+sqrt%7B3%7D+%29%3D+frac%7B1%7D%7B-1%7D%2Alog_%7B75%7D%7D%2875%2A+sqrt%7B3%2A5%5E2%7D+%29%3D+%5C%0A%3D-log_%7B75%7D%2875%2A+sqrt%7B75%7D+%29%3D-%5Blog_%7B75%7D%2875%29%2Blog_%7B75%7D%2875%5E+frac%7B1%7D%7B2%7D+%29%5D%3D%5C%0A%3D-%5B1%2B+frac%7B1%7D%7B2%7D%2Alog_%7B75%7D%2875%29+%5D%3D-%281%2B+frac%7B1%7D%7B2%7D+%29%3D-+frac%7B3%7D%7B2%7D+)
2.![(log_{11}(8)-1)*(1-log_{8}(88))=(log_{11}(8)-1)*(1-log_{8}(8*11))=\
=(log_{11}(8)-1)*(1-[log_{8}(8)+log_{8}(11)])=\
=(log_{11}(8)-1)*(1-[1+log_{8}(11)])=\
=(log_{11}(8)-1)*(1-1-log_{8}(11))=-log_8(11)*(log_{11}(8)-1)=\
=-log_8(11)*log_{11}(8)+log_8(11)=- log_8(11)*frac{1}{log_8(11)} +log_8(11)=\
=-1+log_8(11) (log_{11}(8)-1)*(1-log_{8}(88))=(log_{11}(8)-1)*(1-log_{8}(8*11))=\
=(log_{11}(8)-1)*(1-[log_{8}(8)+log_{8}(11)])=\
=(log_{11}(8)-1)*(1-[1+log_{8}(11)])=\
=(log_{11}(8)-1)*(1-1-log_{8}(11))=-log_8(11)*(log_{11}(8)-1)=\
=-log_8(11)*log_{11}(8)+log_8(11)=- log_8(11)*frac{1}{log_8(11)} +log_8(11)=\
=-1+log_8(11)](https://tex.z-dn.net/?f=%28log_%7B11%7D%288%29-1%29%2A%281-log_%7B8%7D%2888%29%29%3D%28log_%7B11%7D%288%29-1%29%2A%281-log_%7B8%7D%288%2A11%29%29%3D%5C%0A%3D%28log_%7B11%7D%288%29-1%29%2A%281-%5Blog_%7B8%7D%288%29%2Blog_%7B8%7D%2811%29%5D%29%3D%5C%0A%3D%28log_%7B11%7D%288%29-1%29%2A%281-%5B1%2Blog_%7B8%7D%2811%29%5D%29%3D%5C%0A%3D%28log_%7B11%7D%288%29-1%29%2A%281-1-log_%7B8%7D%2811%29%29%3D-log_8%2811%29%2A%28log_%7B11%7D%288%29-1%29%3D%5C%0A%3D-log_8%2811%29%2Alog_%7B11%7D%288%29%2Blog_8%2811%29%3D-+log_8%2811%29%2Afrac%7B1%7D%7Blog_8%2811%29%7D+%2Blog_8%2811%29%3D%5C%0A%3D-1%2Blog_8%2811%29)
3.
2.
3.
Приложения:
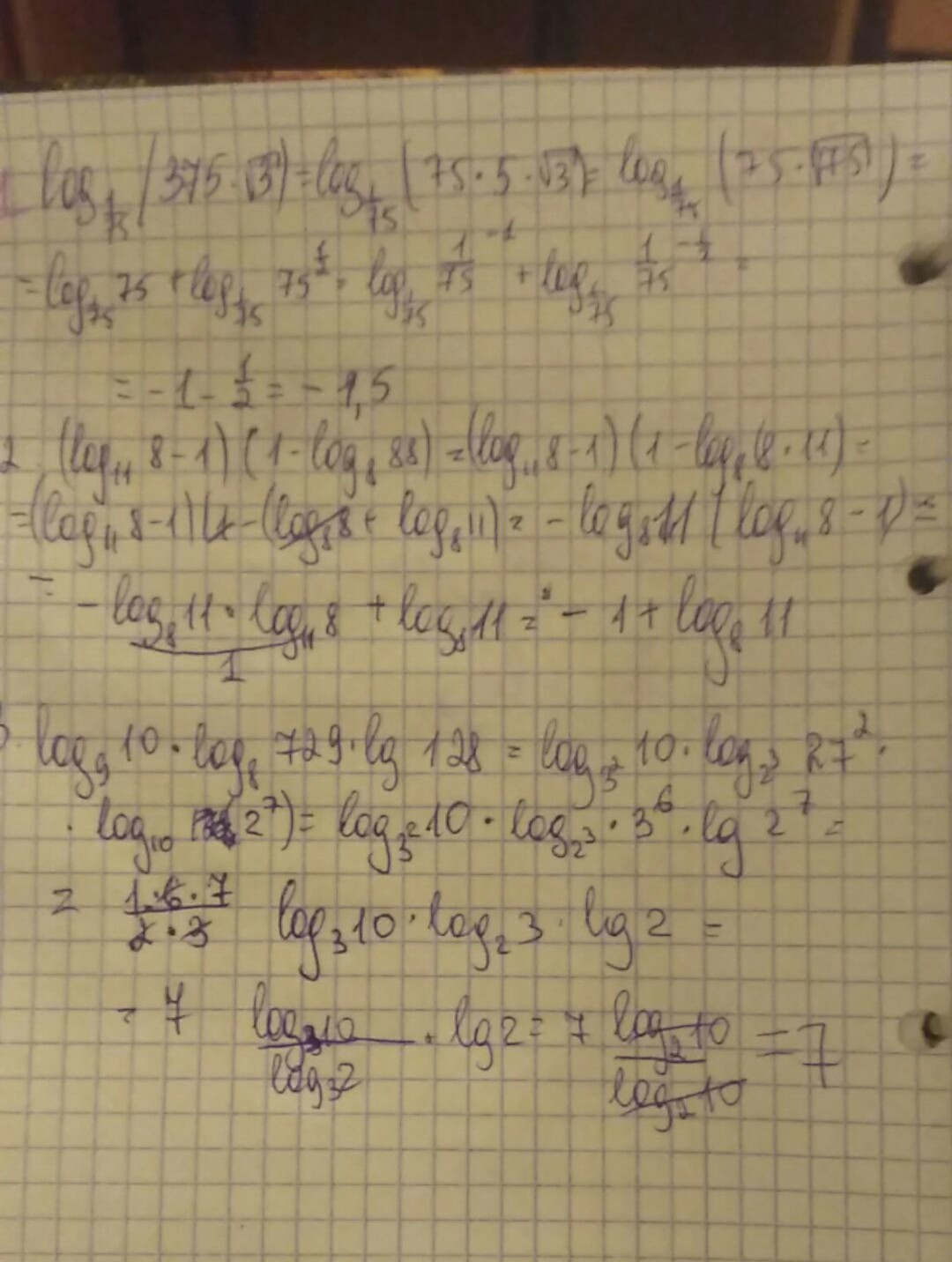
Похожие вопросы
Предмет: Физика,
автор: Аноним
Предмет: Физика,
автор: thill3410
Предмет: Обществознание,
автор: lili1085
Предмет: Математика,
автор: dxcbf
Предмет: Алгебра,
автор: Ириша000