Предмет: Алгебра,
автор: hello93
задание на фото . с подробным решением
Приложения:
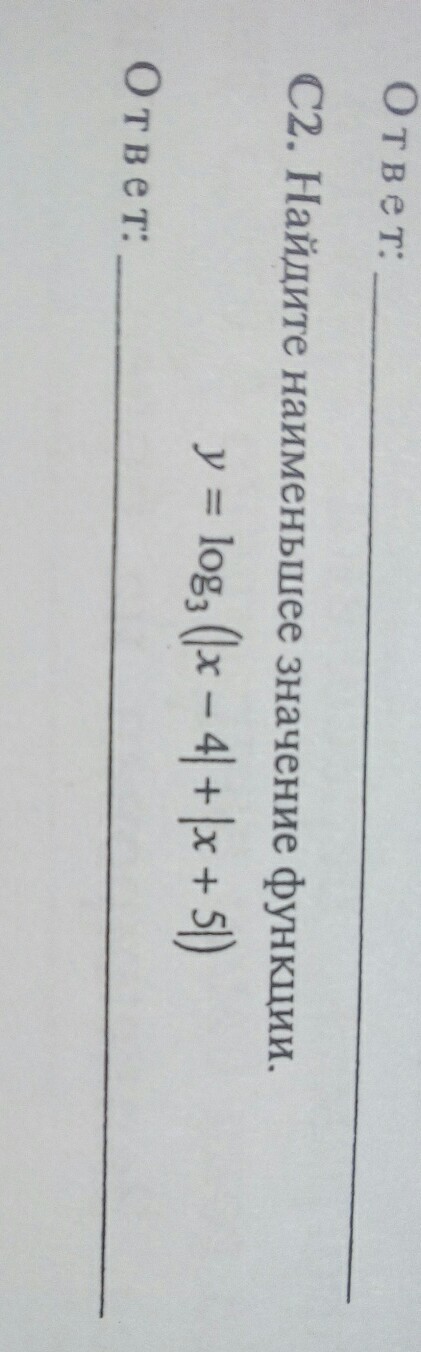
Ответы
Автор ответа:
0
рассмотрим функцию при разных значениях ее аргумента х (числовая ось разбивается нулями подмодульных выражений, а именно
этот логарифм существует при условии
Вывод: на интервале
-----------------------------------------------------------
при значении аргумента
-----------------------------------------------------------
на интервале
-----------------------------------------------------------
при значении аргумента
-----------------------------------------------------------
y(x)=log_3(x-4+x+5)=log_3(2x+1)
этот логарифм существует при условии
Вывод: на интервале
--------------------------------------------
--------------------------------------------
Итого:
теперь же не сложно убедиться, что при
Вот и получаем, что минимальное значение функции равно
Похожие вопросы
Предмет: Қазақ тiлi,
автор: sagybaialtynai
Предмет: Русский язык,
автор: nurbolzautbek09
Предмет: Русский язык,
автор: katyakwlz
Предмет: Химия,
автор: nikolaevamarus
Предмет: Математика,
автор: Gamer111111