Question

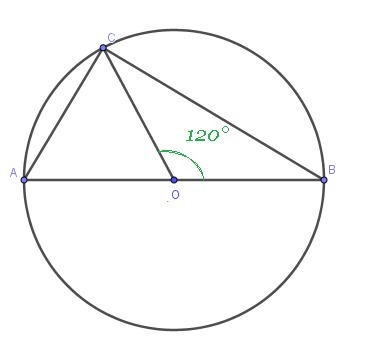
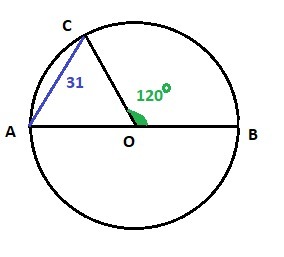
В окружности с центром O проведён диаметр AB и взята точка C так,что угол COB равен 120 градусов,CA=31. Найдите диаметр окружности

Answer 1

ОВ, ОС - радиус, следовательно, OB = OC, значит треугольник BOC - равнобедренный. У равнобедренного треугольника углы при основании равны, то есть: $tt angle OCB=angle OBC=dfrac{180^circ-120^circ}{2} =30^circ$

Вписанные углы, опирающиеся на диаметр, прямые, следовательно, $tt angle ACB=90^circ$, а значит для треугольника AOC: $tt angle ACO=90^circ-30^circ=60^circ$ и $tt angle AOC=60^circ$ ⇒ АОС - равносторонний треугольник. AC = AO = CO = 31

AB = 2AO = 2 * 31 = 62

Ответ: 62.

Answer 2

∠COB = 120°, ∠AOC - смежный углу COB ⇒

∠AOC = 180° - 120° = 60°

∠COB - внешний угол ΔAOC равен сумме двух внутренних углов, не смежных с ним ⇒ ∠CAO + ∠ACO = 120°

ΔAOC - равнобедренный, так как OA = OC - радиусы ⇒

∠CAO = ∠ACO = 120° / 2 = 60°

∠CAO = ∠ACO = ∠AOC = 60° ⇒ ΔAOC - равносторонний ⇒

AO = CA = 31 ⇒ AB = 2AO = 2*31 = 62

Диаметр окружности равен 62