Предмет: Геометрия,
автор: Dan658756
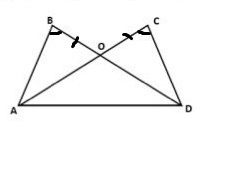
На рисунке угол В = углу С, BO = CO. Докажите что треугольник AOD равнобедренный.
Приложения:
Ответы
Автор ответа:
0
Рассмотрим треугольники АОВ и СОD:
∠В = ∠С и ВО = СО по условию,
∠АОВ = ∠COD (вертикальные углы равны)
Следовательно, ΔАОВ = ΔСОD по стороне и прилежащим к ней углам.
В равных треугольниках соответствующие стороны равны, отсюда:
АО = ОD, следовательно ΔАОD - равнобедренный, что и требовалось доказать.
∠В = ∠С и ВО = СО по условию,
∠АОВ = ∠COD (вертикальные углы равны)
Следовательно, ΔАОВ = ΔСОD по стороне и прилежащим к ней углам.
В равных треугольниках соответствующие стороны равны, отсюда:
АО = ОD, следовательно ΔАОD - равнобедренный, что и требовалось доказать.
Автор ответа:
0
спасиб
Автор ответа:
0
АО=ОD или AO = OB скажите пожалуйста
Автор ответа:
0
АО=OD
Автор ответа:
0
АО=ОD, это видно по рисунку и еще в вышеперичисленном доказано
Похожие вопросы
Предмет: Математика,
автор: asia280983asia
Предмет: Українська мова,
автор: henmuk4
Предмет: Математика,
автор: fgikbddyio
Предмет: Математика,
автор: 87783625053