с подробным решением:
1. Даны векторы а=-2i+j,b(10,-15) и вектор с= вектор 3а - одна пятая вектор b . Найдите коор- динаты и длину вектора c .
2. Напишите уравнение окружности с центром в точке О и прохо- дящей через точку Х, если известно, что О (1; –7), Х (–3; –4).
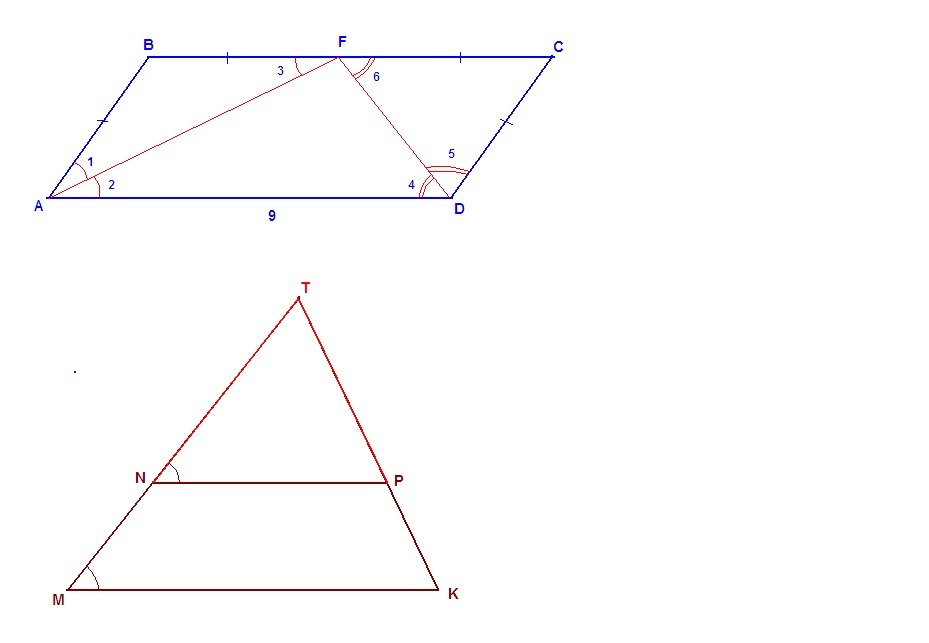
3. В параллелограмме АВСD биссектрисы углов А и D пересекаются
в точке F, лежащей на стороне ВС. Найдите периметр параллелограмма АВСD, если известно, что АD = 9 см.
4. В трапеции MNPK ( MK NP ) продолжения боковых сторон MN и
KP пересекаются в точке Т. а) Докажите, что треугольники NTP и
MTK подобны. б) Найдите площадь треугольника TMK, если известно, что TN : NM = 5 : 3, а площадь треугольника NTP равна 75
Ответы
1. ↑a = - 2↑i + ↑j
↑a = { - 2; 1 } ↑b = { 10 ; - 15 }
↑c = 3↑a - 1/5↑b
3↑a = { 3 · (- 2); 3 · 1 } = { - 6; 3 }
- 1/5↑b = {- 1/5 · 10 ; - 1/5 · (- 15) } = {- 2 ; 3}
↑c = {- 6 - 2; 3 + 3} = {- 8 ; 6}
|↑c| = √((-8)² + 6²) = √(64 + 36) = √100 = 10
2. Уравнение окружности: (x - x₀)² + (y - y₀)² = R², где
(х₀; у₀) - координаты центра, R - радиус окружности.
Подставим координаты центра и координаты точки Х:
(- 3 - 1)² + (- 4 - (- 7))² = R²
R² = (- 4)² + 3² = 16 + 9 = 25
(x - 1)² + (y + 7)² = 25
3. ∠1 = ∠2, так как AF биссектриса ∠А, ∠2 = ∠3 какнакрест лежащие при пересечении параллельных прямых ВС и AD секущей AF, ⇒
∠1 = ∠3, ⇒ ΔАВF равнобедренный, ⇒ АВ = BF.
∠4 = ∠5, так как DF - биссектриса ∠D, ∠5 = ∠6 как накрест лежащие при пересечении параллельных прямых ВС и AD секущей DF, ⇒
∠4 = ∠6, ⇒ Δ DCF равнобедренный, ⇒ DC = CF.
Так как АВ = DC по свойству параллелограмма, то
BF = FC= 1/2 AD = 1/2 · 9 = 4,5 см.
АВ = DC = BF = FC = 4,5 см.
Pabcd = (AB + AD) ·2 = (9 + 4,5) · 2 = 27 см
4. а) ∠ТМК = ∠TNP как соответственные при пересечении параллельных прямых МК и NP секущей МТ, угол при вершине Т общий для треугольников NTP и МТК, значит эти треугольники подобны по двум углам.
б) Если TN : NM = 5 : 3, то коэффициет подобия
k = TN : TM = 5 : 8.
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Stmk : Snpt = 64 : 25
Stmk = 64 · Snpt / 25 = 64 · 75 / 25 = 64 · 3 = 192 кв. ед.