Предмет: Геометрия,
автор: feijoa
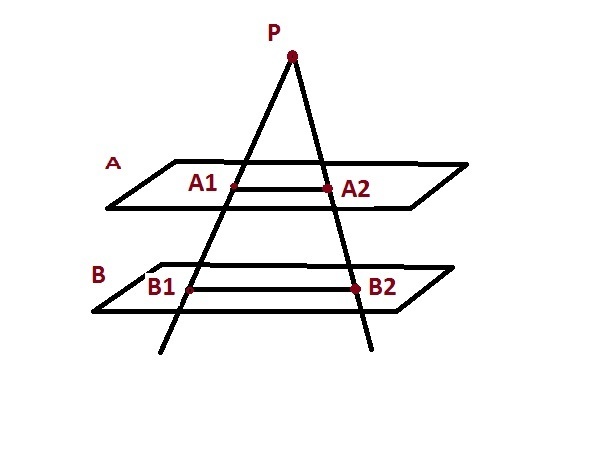
Даны две параллельные плоскостии и не лежащая между ними точка Р. Две прямые, проходящие через точку Р, пересекают ближнюю к точке Р плоскость в точках А₁ и А₂, а дальнюю в точках В₁ и В₂ соответственно. Найдите длину отрезка В₁В₂, если А₁А₂=6 см и РА₁÷А₁В₁=3÷2. Помогите пожалуйста!!!
Ответы
Автор ответа:
0
Поскольку пл-ть А || пл-ти В и точки А1 и В1 принадлежат прямой РВ1, аналогично точк А2 и В2 принадлежат прямой РВ2, то прямая А1А2 || В1В2.
Тогда РВ2 является секущей для параллельных прямых А1А2 и В1В2, тогда угол РА1А2 = углу РВ1В2 как соответственные.
Аналогично РВ2 - секущая для параллельных прямых А1А2 и В1В2, тогда углы РА2 и РВ2 равны как соответственные,
тогда треугольники РА1А2 и РВ1В2 подобны по трем углам (т.к. угол Р общий) и два других соответственно равны.
поскольку из условия дано что РА1/А1В1 = 3/2, то
РВ1/РА1 = (РА1+А1В1)/РА1 = 5/3, тогда
В1В2 = (РВ1/РА1) * А1А2 = (5/3) * 6 = 10 см
Ответ: В1В2 = 10 см.
Тогда РВ2 является секущей для параллельных прямых А1А2 и В1В2, тогда угол РА1А2 = углу РВ1В2 как соответственные.
Аналогично РВ2 - секущая для параллельных прямых А1А2 и В1В2, тогда углы РА2 и РВ2 равны как соответственные,
тогда треугольники РА1А2 и РВ1В2 подобны по трем углам (т.к. угол Р общий) и два других соответственно равны.
поскольку из условия дано что РА1/А1В1 = 3/2, то
РВ1/РА1 = (РА1+А1В1)/РА1 = 5/3, тогда
В1В2 = (РВ1/РА1) * А1А2 = (5/3) * 6 = 10 см
Ответ: В1В2 = 10 см.
Приложения:
Автор ответа:
0
Спасибо большое!!!!
Похожие вопросы
Предмет: Математика,
автор: Llfsskhdxv
Предмет: Алгебра,
автор: Аноним
Предмет: Русский язык,
автор: gugamigurisar
Предмет: История,
автор: lika0012