Предмет: Геометрия,
автор: kuangalieva2018
Заполните пропуски в решении:
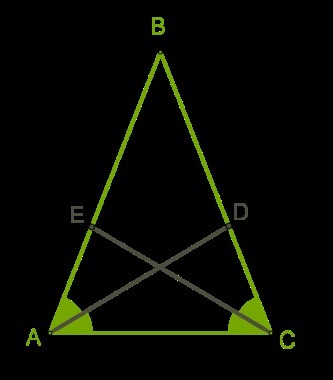
Задача: В равнобедренном треугольнике проведены биссектрисы углов, прилежащих к основанию. Определи длину биссектрисы угла ∡A, если длина биссектрисы угла ∡C равна 12 см.
Рассмотрим треугольникиΔDAC и Δ___
.
1. Углы, прилежащие к основанию равнобедренного треугольника,
. Так как данный треугольник равнобедренный, то∡
=∡BCA.
2. Так как проведены биссектрисы этих углов, справедливо, что ∡___
=∡DAC=∡DCE=∡___
3. У рассматриваемых треугольников общая сторона__
.
Значит треугольники равны по второму признаку равенства треугольников.
У равных треугольников равны все соответствующие элементы, в том числе стороны
__=__
Длина искомой биссектрисы равна
__см.
Приложения:
Ответы
Автор ответа:
0
Ответ: 12 см
Объяснение:
Рассмотрим треугольники ΔDAC и ΔЕСА:
1. Углы, прилежащие к основанию равнобедренного треугольника, равны.
Так как данный треугольник равнобедренный, то ∠ВАС = ∠BCA.
2. Так как проведены биссектрисы этих углов, справедливо, что
∠EAD = ∠DAC = ∠DCE = ∠ЕСА.
3. У рассматриваемых треугольников общая сторона АС.
Значит треугольники равны по второму признаку равенства треугольников.
У равных треугольников равны все соответствующие элементы, в том числе стороны
AD = CE = 12 cм.
Длина искомой биссектрисы равна
12 см.
Похожие вопросы
Предмет: Математика,
автор: nurisumrov
Предмет: Русский язык,
автор: davidstonda9
Предмет: Английский язык,
автор: adiarymbaeva
Предмет: Алгебра,
автор: вика348
Предмет: Физика,
автор: Sv190715