Предмет: Геометрия,
автор: user15042001
Пожалуйста, помогите с заданием 15 по геометрии,решите подробно,
15 баллов
Задание на фото:
Приложения:
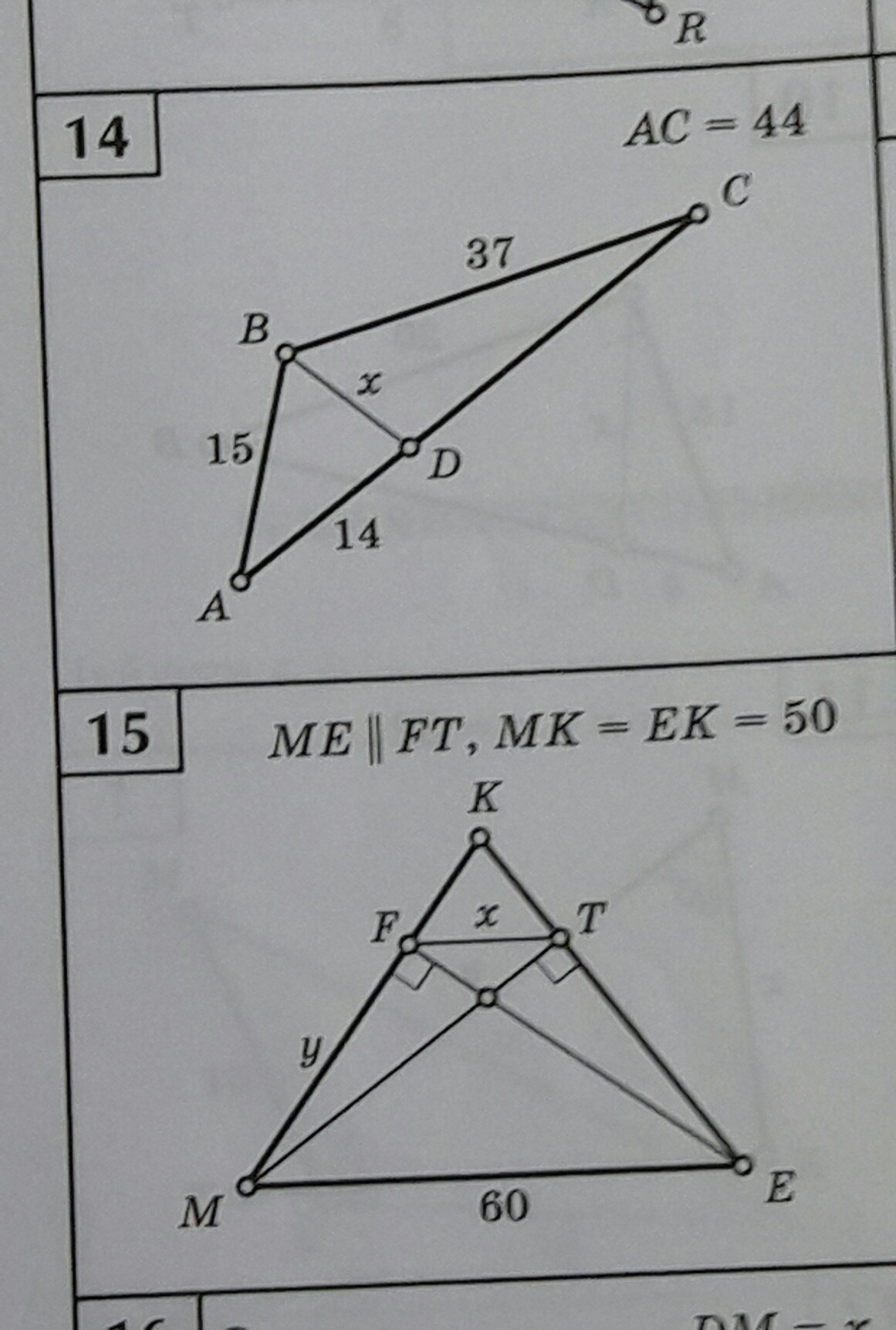
Ответы
Автор ответа:
0
Из ΔМКE по теореме косинусов:

ΔМКE равнобедренный, отсюда:
∠КМЕ = ∠КЕМ = (180 - 73,74)/2 = 53,13°
Из ΔMFE (∠MFE=90°):

FK = MK - y = 50 - 36 = 14
ME || FT по условию, следовательно:
КТ = FK = 14
Из ΔFКT по теореме косинусов:

ΔМКE равнобедренный, отсюда:
∠КМЕ = ∠КЕМ = (180 - 73,74)/2 = 53,13°
Из ΔMFE (∠MFE=90°):
FK = MK - y = 50 - 36 = 14
ME || FT по условию, следовательно:
КТ = FK = 14
Из ΔFКT по теореме косинусов:
Автор ответа:
0
Спасибо, оказывается здесь надо было найти не только сторону, принятую за х, но и решить весь треугольник, не знаю,что делать, но всё равно, большое Вам спасибо)
Автор ответа:
0
task/26916180
--------------------
Проведем высоту KD ⊥ ME , т.к. ΔMKE равнобедренный ,то
MD = ED =ME/2 = 30 ;
Из ΔMKD по теореме Пифагора :
KD=√(MK² -MD²) =√(50² - 30²) = 40.
S(MKE) = ME*KD/2 =MK*EF/2 ⇒ EF =ME*KD / MK =60*40 /50 =48.
Из ΔMKD :
MF=y =√(ME² - EF²) =√(60² -48²) =√4²(15² -12²) =4*9 =36.
---
ΔFKT~ ΔMKE
FT / ME = FK / MK ;
FT =x =(FK / MK)*ME ; * * * FK = MK-MF =50 -36 =14 * * *
FT==x=( 14 / 50 )*60 = 16,8 .
ответ: x =16,8 , y =36.
--------------------
Проведем высоту KD ⊥ ME , т.к. ΔMKE равнобедренный ,то
MD = ED =ME/2 = 30 ;
Из ΔMKD по теореме Пифагора :
KD=√(MK² -MD²) =√(50² - 30²) = 40.
S(MKE) = ME*KD/2 =MK*EF/2 ⇒ EF =ME*KD / MK =60*40 /50 =48.
Из ΔMKD :
MF=y =√(ME² - EF²) =√(60² -48²) =√4²(15² -12²) =4*9 =36.
---
ΔFKT~ ΔMKE
FT / ME = FK / MK ;
FT =x =(FK / MK)*ME ; * * * FK = MK-MF =50 -36 =14 * * *
FT==x=( 14 / 50 )*60 = 16,8 .
ответ: x =16,8 , y =36.
Автор ответа:
0
Спасибо Вам огромное!)
Похожие вопросы