Question

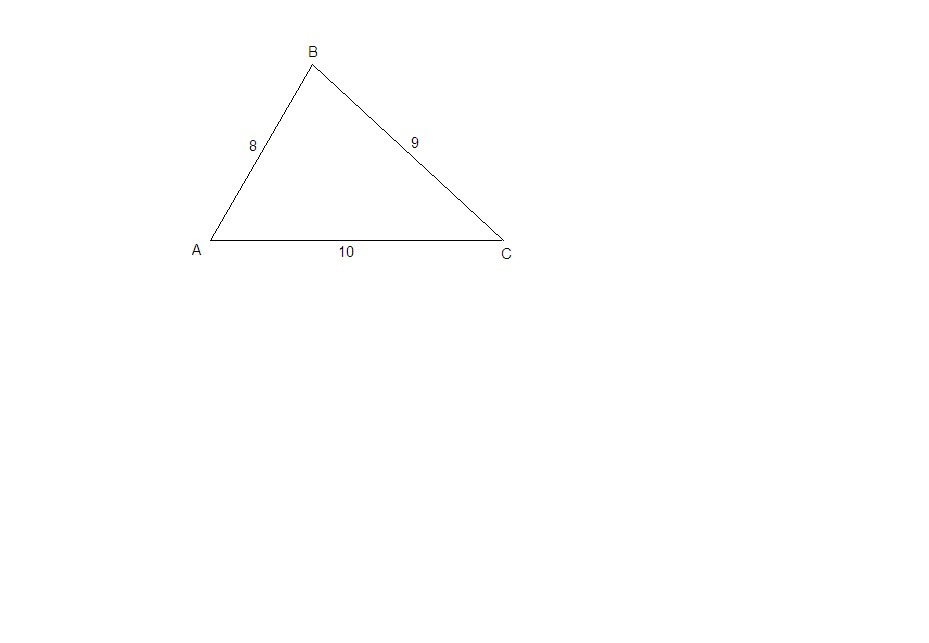
Найдите все три угла треугольника, если стороны равны 10см, 9см и 8 см.

Answer 1

По теореме косинусов:
cos∠B = (BA² + BC² - AC²) / (2·BA·BC)
cos∠B = (64 + 81 - 100) / (2·8·9) = 45/ (2·8·9) = 5/16 = 0,3125
∠B ≈ 71,5°

cos∠A = (AB² + AC² - BC²) / (2·AB·AC)
cos∠A = (64 + 100 - 81) / (2·8·10) = 83 / 160 ≈ 0,5188
∠A ≈ 59°

∠C = 180° - (∠A + ∠B)
∠C ≈ 180° - (59° + 71,5°) ≈ 180° - 130,5° ≈ 49,5°