Question

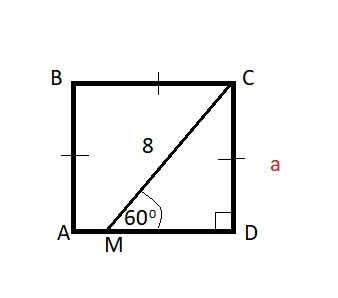
на стороне AD квадрата ABCD отметили точку M так , что угол CMD = 60° . Найдите площадь, если CM = 8см. Ответ в квадратных сантиметрах.

Answer 1

По условию АВСD  - квадрат, следовательно:
АВ=ВС=СD =DA =а
∠A = ∠B =∠C=∠D = 90°
S = a², где а -  сторона квадрата

Рассмотрим прямоугольный Δ СDM (∠D = 90°) :
CМ = 8  -  гипотенуза
СD,DM -  катеты
Сумма острых углов прямоугольного треугольника равна 90°, следовательно:  
∠СМD + ∠MCD = 90° ⇒ ∠MCD = 90° -∠CMD
∠МСD = 90 - 60  = 30°
Катет, лежащий против угла в 30° равен половине гипотенузы:
MD =  ¹/₂* CM 
МD = ¹/₂ * 8  =  4 см
По теореме Пифагора : 
СМ²  = CD² + МD²   ⇒  CD= √(CM² - CD²) 
CD = √ (8² - 4²) = √ (64 - 16)  = √48  = √(16*3) = 4√3 см  ⇒  а=4√3 (см)

Площадь квадрата АВСD :
S кв. = (4√3) ²  = (√48)²  = 48 ( см² )

ОТВЕТ : S кв. = 48 см²