Question

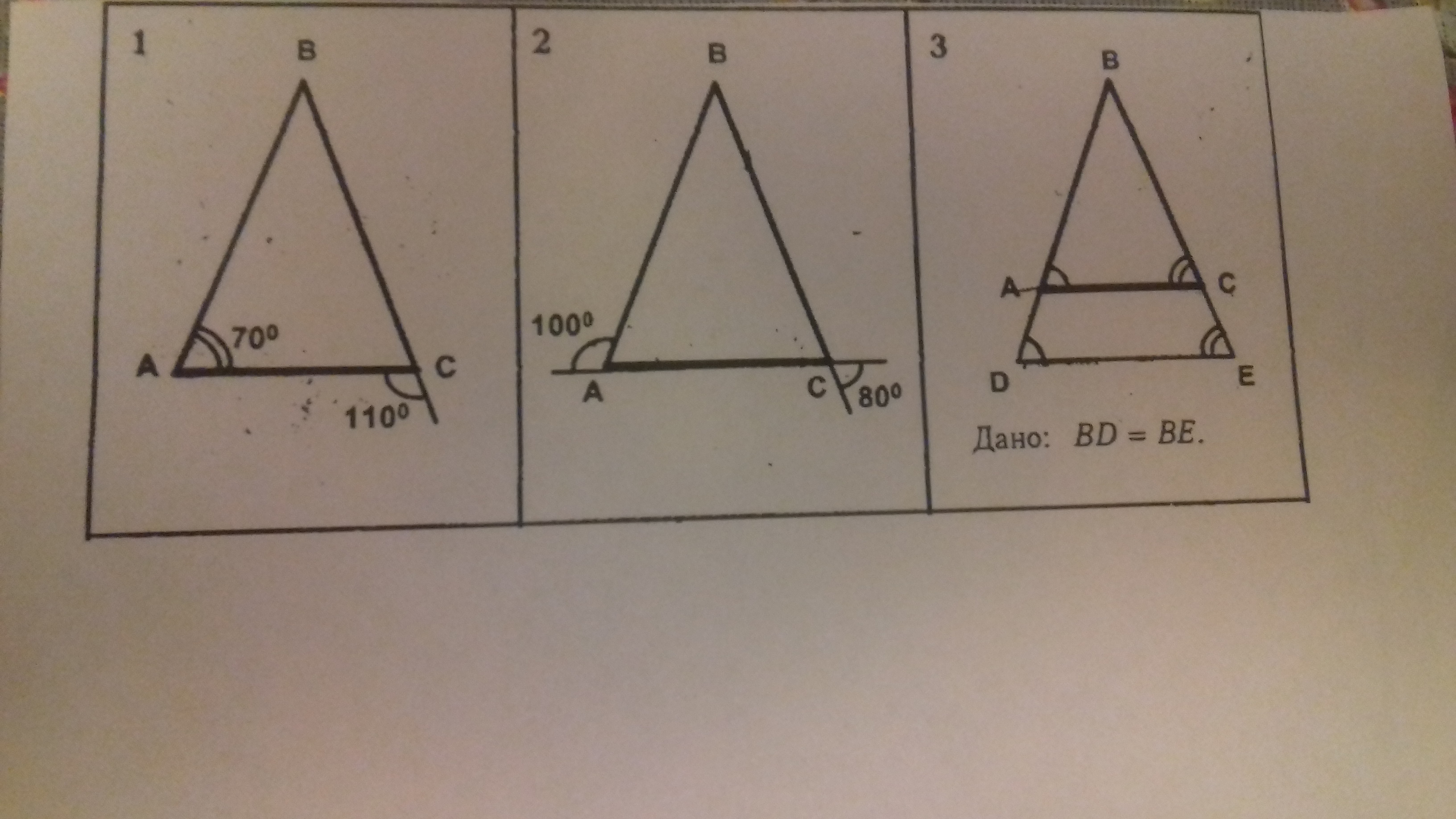
Везде надо доказать, что ABC- равнобедренный треугольник.

Answer 1

1. Внешний угол при С равен 110°. Найдем смежный угол:
∠ВСА = 180 - 110 = 70°
Видим, что ∠ВАС = ∠ВСА. Если два угла треугольника равны, то такой треугольник равнобедренный.

2. Аналогично. Внешний угол при А = 100°. Ищем смежный угол:
∠ВАС = 180 - 100 = 80°
Внешний угол при С и ∠ВСА равны, так как они вертикальные. Опять получаем два равных угла, следовательно, треугольник равнобедренный.

3. ΔDBE и ΔАВС подобны по двум углам. Если в ΔDBE по условию две стороны равны, то в ΔАВС, соответственно, две стороны также равны. Если две стороны равны, то треугольник равнобедренный.