Предмет: Геометрия,
автор: JaikHit533
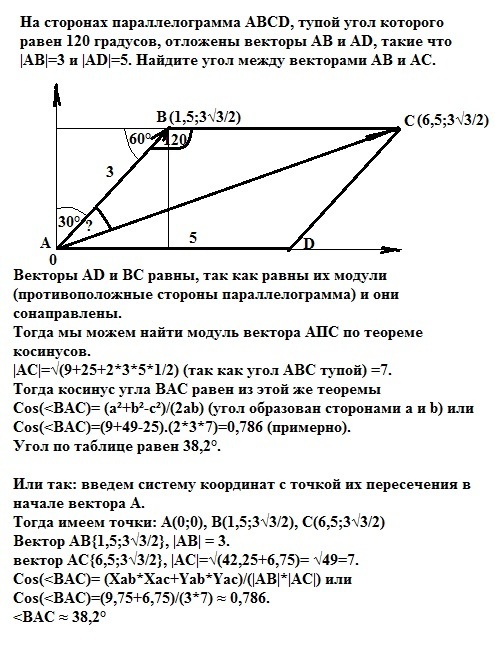
На сторонах параллелограмма ABCD, тупой угол которого равен 120 градусов, отложены векторы AB и AD, такие что |AB|=3 и |AD|=5. Найдите угол между векторами AB и AC.
Ответы
Автор ответа:
0
Векторы AD и ВС равны, так как равны их модули (противоположные стороны параллелограмма) и они сонаправлены.
Тогда мы можем найти модуль вектора АПС по теореме косинусов.
|АС|=√(9+25+2*3*5*1/2) (так как угол АВС тупой) =7.
Тогда косинус угла ВАС равен из этой же теоремы
Cos(<BAC)= (a²+b²-c²)/(2ab) (угол образован сторонами а и b) или
Cos(<BAC)=(9+49-25).(2*3*7)=0,786 (примерно).
Угол по таблице равен 38,2°.
Или так: введем систему координат с точкой их пересечения в начале вектора А.
Тогда имеем точки: А(0;0), В(1,5;3√3/2), С(6,5;3√3/2)
Вектор AВ{1,5;3√3/2}, |AB| = 3.
вектор АС{6,5;3√3/2}, |AC|=√(42,25+6,75)= √49=7.
Угол между векторами равен скалярному произведению этих векторов, деленному на протзведение их модулей.
Cos(<BAC)= (Xab*Xac+Yab*Yac)/(|AB|*|AC|) или
Cos(<BAC)=(9,75+6,75)/(3*7) ≈ 0,786.
<BAC ≈ 38,2°
Тогда мы можем найти модуль вектора АПС по теореме косинусов.
|АС|=√(9+25+2*3*5*1/2) (так как угол АВС тупой) =7.
Тогда косинус угла ВАС равен из этой же теоремы
Cos(<BAC)= (a²+b²-c²)/(2ab) (угол образован сторонами а и b) или
Cos(<BAC)=(9+49-25).(2*3*7)=0,786 (примерно).
Угол по таблице равен 38,2°.
Или так: введем систему координат с точкой их пересечения в начале вектора А.
Тогда имеем точки: А(0;0), В(1,5;3√3/2), С(6,5;3√3/2)
Вектор AВ{1,5;3√3/2}, |AB| = 3.
вектор АС{6,5;3√3/2}, |AC|=√(42,25+6,75)= √49=7.
Угол между векторами равен скалярному произведению этих векторов, деленному на протзведение их модулей.
Cos(<BAC)= (Xab*Xac+Yab*Yac)/(|AB|*|AC|) или
Cos(<BAC)=(9,75+6,75)/(3*7) ≈ 0,786.
<BAC ≈ 38,2°
Приложения:
Похожие вопросы
Предмет: Обществознание,
автор: danilamihajlovic72
Предмет: Русский язык,
автор: nniko75
Предмет: Английский язык,
автор: vasikoksana
Предмет: Физика,
автор: Аноним
Предмет: Биология,
автор: Ойдин