Предмет: Математика,
автор: ilemesovadar
Помогите пожалуйста! Буду очень благодарна❤
Приложения:

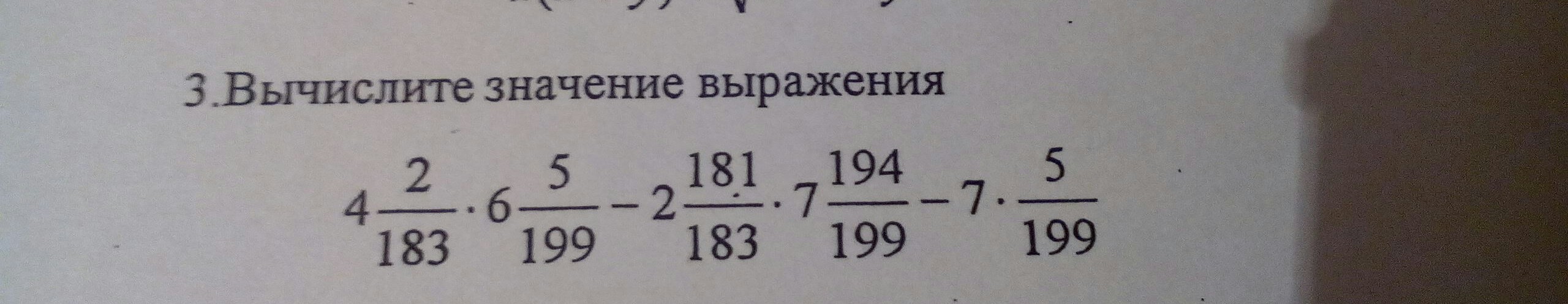

Ответы
Автор ответа:
0
Рассмотрим наибольшие из n+1 выбранных чисел . По условию, оно меньше, чем 2n. Рассмотрим " наихудший" вариант, когда это число принимает наибольшее значение, то есть равно 2n-1.
Все предыдущие 2n-2 чисел ряда на n-1 "ящиков" следующим образом:
l 1 2n-2
ll 2 2n-3
lll 3 2n-4
..... ..... .........
n-1 n-1 n
Сумма чисел в каждом "ящике" равна 2n-1, то есть, равна наибольшему из n+1 выбор. чисел.
Выберем из n-1 "ящиков" оставшиеся n чисел (одно мы уже выбрали - наибольшее). По принципу 2n-1. Итак, нашлись три числа, сумма двух из которых равна третьему.
Во всех остальных вариантах "ящиков" будет меньше, чем n-1, a" придметов - по прежнему n. Значит, в этом случае тем более найдутся два числа , сумма которых равна третьему - наибольшему числу.
Все предыдущие 2n-2 чисел ряда на n-1 "ящиков" следующим образом:
l 1 2n-2
ll 2 2n-3
lll 3 2n-4
..... ..... .........
n-1 n-1 n
Сумма чисел в каждом "ящике" равна 2n-1, то есть, равна наибольшему из n+1 выбор. чисел.
Выберем из n-1 "ящиков" оставшиеся n чисел (одно мы уже выбрали - наибольшее). По принципу 2n-1. Итак, нашлись три числа, сумма двух из которых равна третьему.
Во всех остальных вариантах "ящиков" будет меньше, чем n-1, a" придметов - по прежнему n. Значит, в этом случае тем более найдутся два числа , сумма которых равна третьему - наибольшему числу.
Похожие вопросы
Предмет: Геометрия,
автор: asanov072
Предмет: Английский язык,
автор: aboba8812
Предмет: Алгебра,
автор: zlataart2308
Предмет: Математика,
автор: Luciyaok