Question

Помогите определить,сколько решений имеет система

Answer 1

Расписываю очень подробно:

$left { {{y= sqrt{16-x^{2}} } atop {y-x=4}} right.$
$y= sqrt{16-x^{2}} =y-x=4, y-(y-x)= sqrt{16-x^{2}}-4$
$sqrt{16-x^{2}}=x+4$
$(x+4)^{2}= x^{2} +2x*4*4^{2}$ => упрощаем:
$= x^{2} +8x+ 4^{2} = x^{2} +8x+16$
$16-x^{2}=x^{2}+8x+16$
$16-x^{2}-(x^{2}+8x+16)=x^{2}+8x+16-(x^{2}+8x+16)$ => упрощаем:
$-(x^{2}+8x+16)=-(x^{2})-(8x)-(16)=-x^{2}-8x-16$
$=16-x^{2}-x^{2}-8x-16$ => упрощаем:
$=16-2x^{2}-8x-16=-2x^{2}-8x+16-16=-2x^{2}-8x$
$x^{2}+8x+16-(x^{2}+8x+16)=0$
$-2x^{2}-8x=0$
$x= frac{-(-8)+ sqrt{(-8)^{2}-4(-2)*0} }{2(-2)}$
$= frac{8+ sqrt{(-8)^{2}-4(-2)*0} }{-2*2}$
$= frac{8+ sqrt{(-8)^{2}-(-2)*0*4} }{-4}$
$8+ sqrt{(-8)^{2}-4(-2)*0}= sqrt{(-8)^{2}+0*2*4}= sqrt{64+0} = sqrt{64}$
$=8+ sqrt{64} = frac{8+ sqrt{64} }{-4}$
$= -frac{8+ sqrt{64} }{4} , sqrt{64} =8$
$=- frac{8+8}{4} =- frac{16}{4} =-4$

$x= frac{-(-8)- sqrt{(-8)^{2}-4(-2)*0}}{2(-2)} = frac{8- (sqrt{8})^{2}-4(-2)*0 }{-2*2}$
$= frac{8- sqrt{(-8)^{2}-(-2)*0*4} }{-4}$
$8- sqrt{(-8)^{2}-4(-2)*0}= sqrt{(-8)^{2}+0*2*4}= sqrt{64+0} = sqrt{64}$
$8- sqrt{64} =- frac{8- sqrt{64} }{4}$
$=- frac{8-8}{4} =0$
$x=-4, x=0$

А теперь подставим и проверим верны ли найденные корни:
$y= sqrt{16-x^{2}} , y= sqrt{16-(-4)^{2}}$ !при y=0
$y= sqrt{16-4^{2}}$
$y= sqrt{0}$
$y=0$

$y= sqrt{16-x^{2}}, y=4$
$y= sqrt{16-0^{2}}$
$y= sqrt{16-0}$
$y= sqrt{16} = sqrt{4^{2}} =4$
$y=4$

Проверяем решения:
$y= sqrt{16-x^{2}} , y=0$
$= sqrt{16-(-4)^{2}}$
0=0

$y= sqrt{16-x^{2}}, y=4$
$sqrt{16-0^{2}}$
4=4

Т.е. ответ будет:
$boxed {(x=-4;0, y=0;4)}$, то есть система имеет бесконечно много решений.

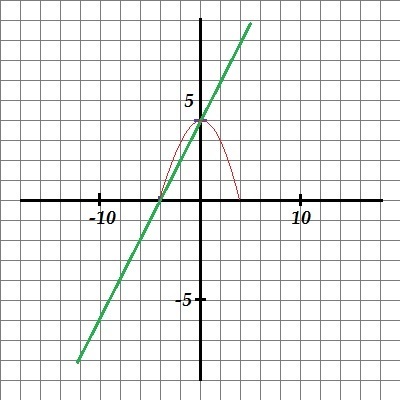
График в приложении (см. фото).