В квадрате 130 × 130 закрашено несколько клеток. В каждой строчке есть либо 1, либо 7 закрашенных клеток, а в каждом столбце есть либо 3, либо 4 закрашенных клетки. Какое наименьшее число клеток может быть закрашено?
Ответы
Обозначим количество строк, в которых закрашена 1 клетка через a, а количество строк, в которых закрашены 7 клеток через b.
Обозначим количество столбцов, в которых закрашены 3 клетки через c, а количество столбцов, в которых закрашены 4 клетки через d.
Общее количество закрашенных красок N может быть выражено двояко:
N = a + 7b = 3c + 4d
Нам нужно найти min(N)
Имеются следующие ограничения и соотношения на a, b, c и d
a, b, c, d ∈ Z, 0 ≤ a,b,c,d ≤ 130, a + b = 130, c + d = 130
Подставим эти соотношения в равенство для N:
a + 7b = 3c + 4d
(a + b) + 6b = 3(c + d) + d
130 + 6b = 3 * 130 + d
d = 6b - 260
Т.к. 0 ≤ d ≤ 130, то:
0 ≤ 6b - 260 ≤ 130
260 ≤ 6b ≤ 390
43.(3) ≤ b ≤ 65
Т.к. нам нужно найти min(N) = min(a + 7b) = min(130 + 6b), то минимум достигается при минимальном b = 44.
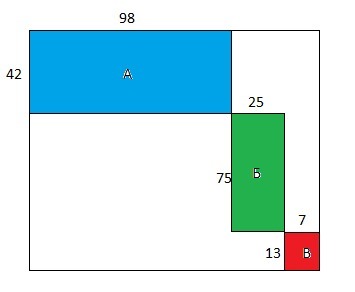
Осталось построить пример, показывающий, что возможна раскраска квадрата 130*130 так, что у него будет раскрашено по 7 клеток в 44 строках, по одной клетке в 86 (130 - 44) строках, по 4 клетки в 4 столбцах (6 * 44 - 260) и по 3 клетки в 126 столбцах (130 - 4), а всего 394 клетки (86 + 7 * 44).
Схема заполнения квадрата показана на рис.1 - будут заполнены только прямоугольники, размеры и расположение которых указаны.
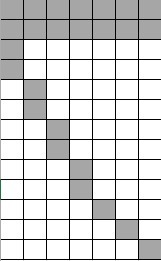
Прямоугольник А будет заполнен так, как указано на рис.2 - 14 блоков каждый размера 3 * 7.
Прямоугольник Б будет заполнен так, как указано на рис.3 - 25 блоков каждый размера 3 * 1.
И наконец прямоугольник В заполнен так, как указано на рис. 3