Предмет: Геометрия,
автор: чебурек51575
от даного луча отложить угол равный одной четверной
даного угла
Ответы
Автор ответа:
0
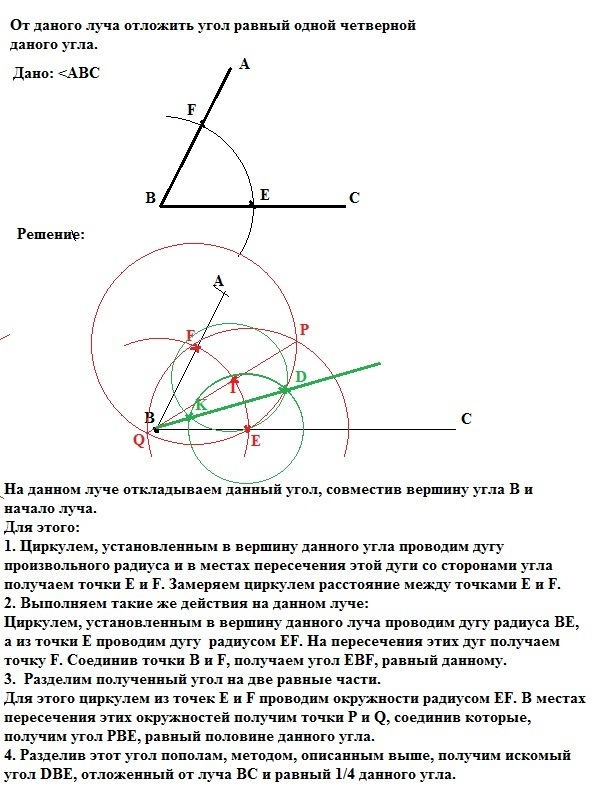
На данном луче ВС откладываем угол, равный данному углу АВС , совместив вершину угла В и начало луча.
Для этого:
1. Циркулем, установленным в вершину данного угла проводим дугу произвольного радиуса и в местах пересечения этой дуги со сторонами угла получаем точки E и F. Замеряем циркулем расстояние между точками E и F.
2. Выполняем такие же действия на данном луче:
Циркулем, установленным в вершину данного луча проводим дугу радиуса ВЕ, а из точки Е проводим дугу радиусом EF. На пересечения этих дуг получаем точку F. Соединив точки В и F, получаем угол EBF, равный данному.
3. Разделим полученный угол на две равные части.
Для этого циркулем из точек Е и F проводим окружности радиусом EF. В местах пересечения этих окружностей получим точки P и Q, соединив которые, получим угол РВЕ, равный половине данного угла.
4. Разделив этот угол пополам, методом, описанным выше, получим искомый угол DBE, отложенный от луча ВС и равный 1/4 данного угла.
Для этого:
1. Циркулем, установленным в вершину данного угла проводим дугу произвольного радиуса и в местах пересечения этой дуги со сторонами угла получаем точки E и F. Замеряем циркулем расстояние между точками E и F.
2. Выполняем такие же действия на данном луче:
Циркулем, установленным в вершину данного луча проводим дугу радиуса ВЕ, а из точки Е проводим дугу радиусом EF. На пересечения этих дуг получаем точку F. Соединив точки В и F, получаем угол EBF, равный данному.
3. Разделим полученный угол на две равные части.
Для этого циркулем из точек Е и F проводим окружности радиусом EF. В местах пересечения этих окружностей получим точки P и Q, соединив которые, получим угол РВЕ, равный половине данного угла.
4. Разделив этот угол пополам, методом, описанным выше, получим искомый угол DBE, отложенный от луча ВС и равный 1/4 данного угла.
Приложения:
Автор ответа:
0
Великолепно )
Похожие вопросы
Предмет: Математика,
автор: tim584822
Предмет: Биология,
автор: winchester0195
Предмет: Литература,
автор: meci3dcheek2
Предмет: Алгебра,
автор: Andreitu