Предмет: Математика,
автор: Bart128
Вычислить несобственный интеграл или указать его расходимость
Приложения:
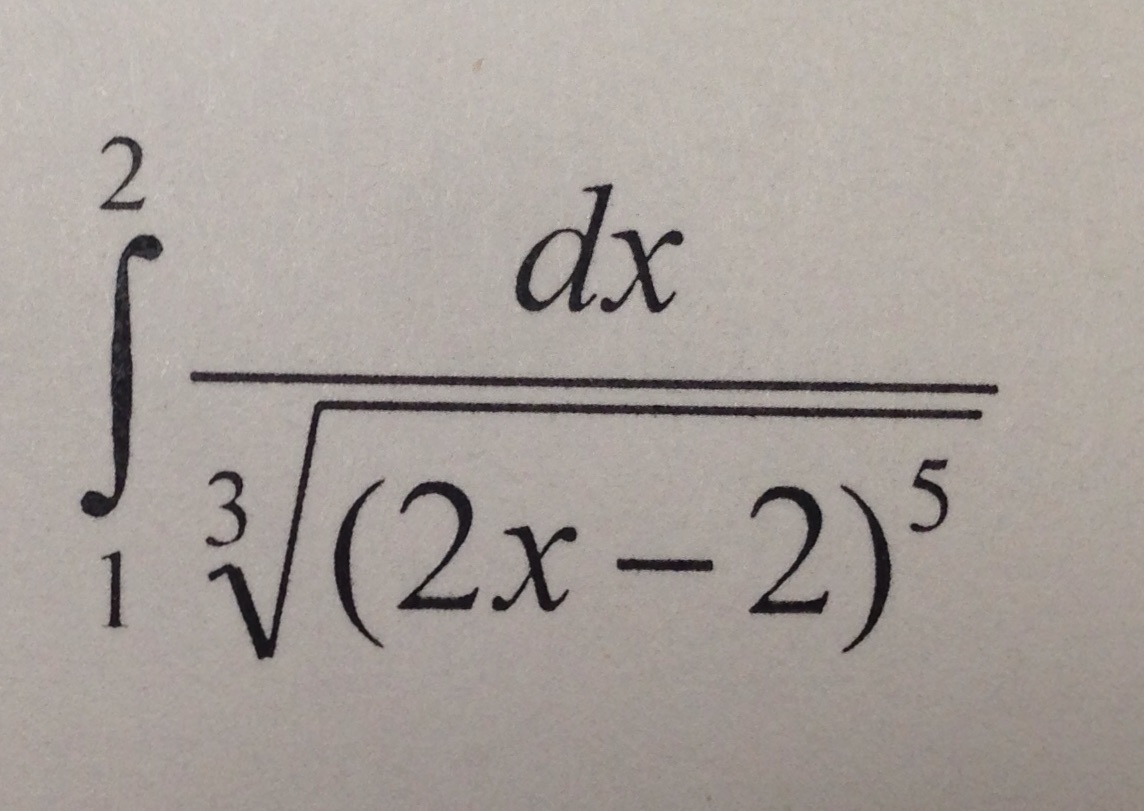
Ответы
Автор ответа:
0
Вроде бы нормальный интеграл, но подынтегральная функция в точке x=1 терпит бесконечный разрыв.
Возьмём интеграл путём приведения дифференциала к виду, когда интеграл станет табличным. Интеграл будем вычислять по формуле Ньютона-Лейбница, правда, модифицированной для несобственных интегралов подобного рода.
Несобственный интеграл расходится.
Похожие вопросы
Предмет: Алгебра,
автор: bikmullintimur52
Предмет: Литература,
автор: winxylia
Предмет: Информатика,
автор: daramironova1234
Предмет: Алгебра,
автор: Сергей3445
Предмет: Алгебра,
автор: ruslansobolev