Предмет: Математика,
автор: Аноним
Из шести стержней длины 3 склеили треугольную пирамиду. На рёбра пирамиды сели три мухи.
Оказалось, что расстояние между каждыми двумя из этих мух (измеряемое кратчайшим путем по рёбрам пирамиды) не меньше R.
При каком наибольшем R такое возможно?
Ответы
Автор ответа:
0
Пусть R > 3, тогда никакие две мухи не сидят на одном ребре. Каждое ребро принадлежит двум граням, значит, из трёх рёбер какие-то два лежат в одной грани (в противном случае граней должно быть не меньше 2 * 3 = 6, а их всего 4. Рассмотрим пути между мухами, которые сидят в этой грани.
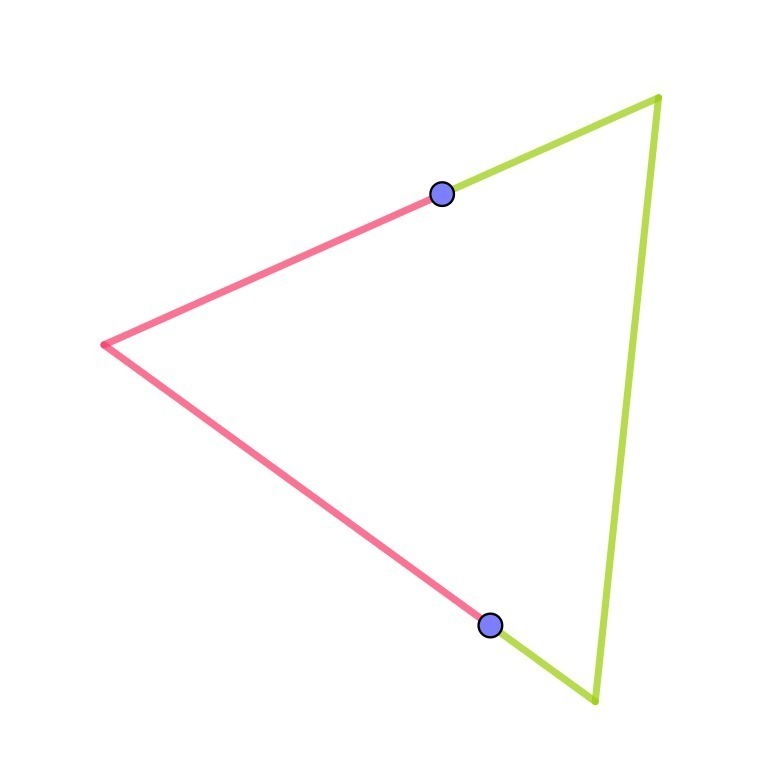
Эта грань — треугольник с периметром P = 3 * 3 = 9. Между мухами, сидящими в этой грани, есть два пути (см. рисунок, красный и зелёный), суммарная длина которых равна 9. Значит, кратчайший путь не длиннее 9/2 = 4,5.
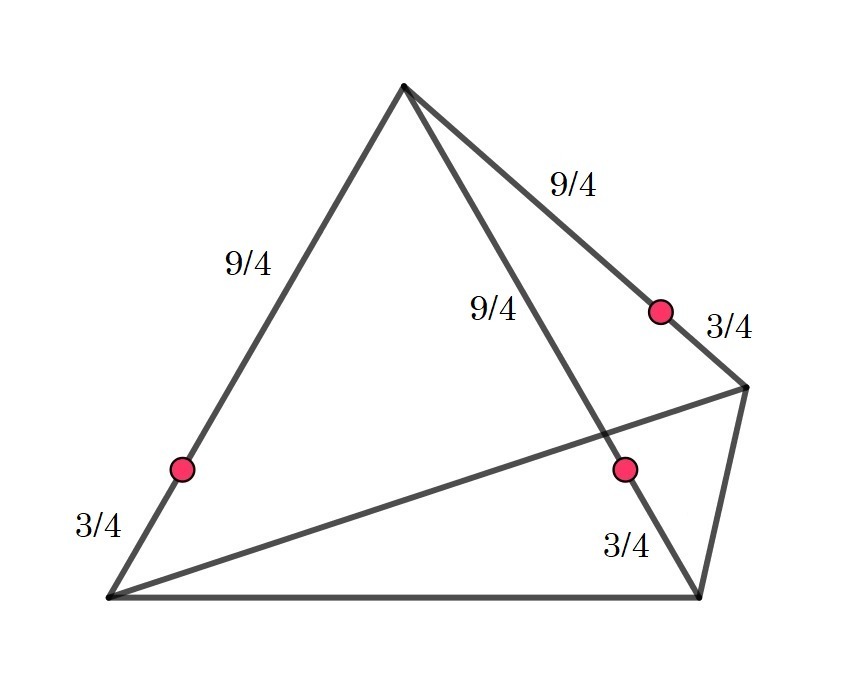
Пример, как могут сидеть мухи, чтобы R было равно 4,5, на второй картинке.
Эта грань — треугольник с периметром P = 3 * 3 = 9. Между мухами, сидящими в этой грани, есть два пути (см. рисунок, красный и зелёный), суммарная длина которых равна 9. Значит, кратчайший путь не длиннее 9/2 = 4,5.
Пример, как могут сидеть мухи, чтобы R было равно 4,5, на второй картинке.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: aaairk228
Предмет: Алгебра,
автор: vitalinasabatin002
Предмет: Геометрия,
автор: alekseynikolaev29381
Предмет: Математика,
автор: Марьяна414