Предмет: Геометрия,
автор: Ананимус22222
Радиус окружности описанной около правильного многоугольника равен 4 корня из 2 а сторона многоугольника 8 см. Найдите: 1) Радиус окружности вписанной в многоугольник 2) Количество сторон многоугольника
Ответы
Автор ответа:
0
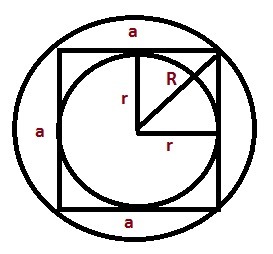
Рассмотрим задачу на данном примере. Построим многоугольник, вписанную и описанную окружность.
Рассмотрим прямоугольный треугольник, образованный двумя радиусами. Тогда по теореме Пифагора R=√(r²+ r²) =√2r²=r√2. Используем условие r√2=4√2 ⇒ r=4√2/√2=4см, тогда сторона нашего многоугольника а=2r=2*4=8см, что соответствует условию, значит количество сторон многоугольника =4
Ответ: Радиус окружности вписанной в многоугольник =4см, количество сторон многоугольника-4.
Рассмотрим прямоугольный треугольник, образованный двумя радиусами. Тогда по теореме Пифагора R=√(r²+ r²) =√2r²=r√2. Используем условие r√2=4√2 ⇒ r=4√2/√2=4см, тогда сторона нашего многоугольника а=2r=2*4=8см, что соответствует условию, значит количество сторон многоугольника =4
Ответ: Радиус окружности вписанной в многоугольник =4см, количество сторон многоугольника-4.
Приложения:
Похожие вопросы
Предмет: География,
автор: pomplyy
Предмет: История,
автор: crazyciller
Предмет: География,
автор: rukiyabulazova
Предмет: Математика,
автор: Аноним