Предмет: Алгебра,
автор: Vkosmos416
Помогите решить уравнение, пожалуйста!
Приложения:
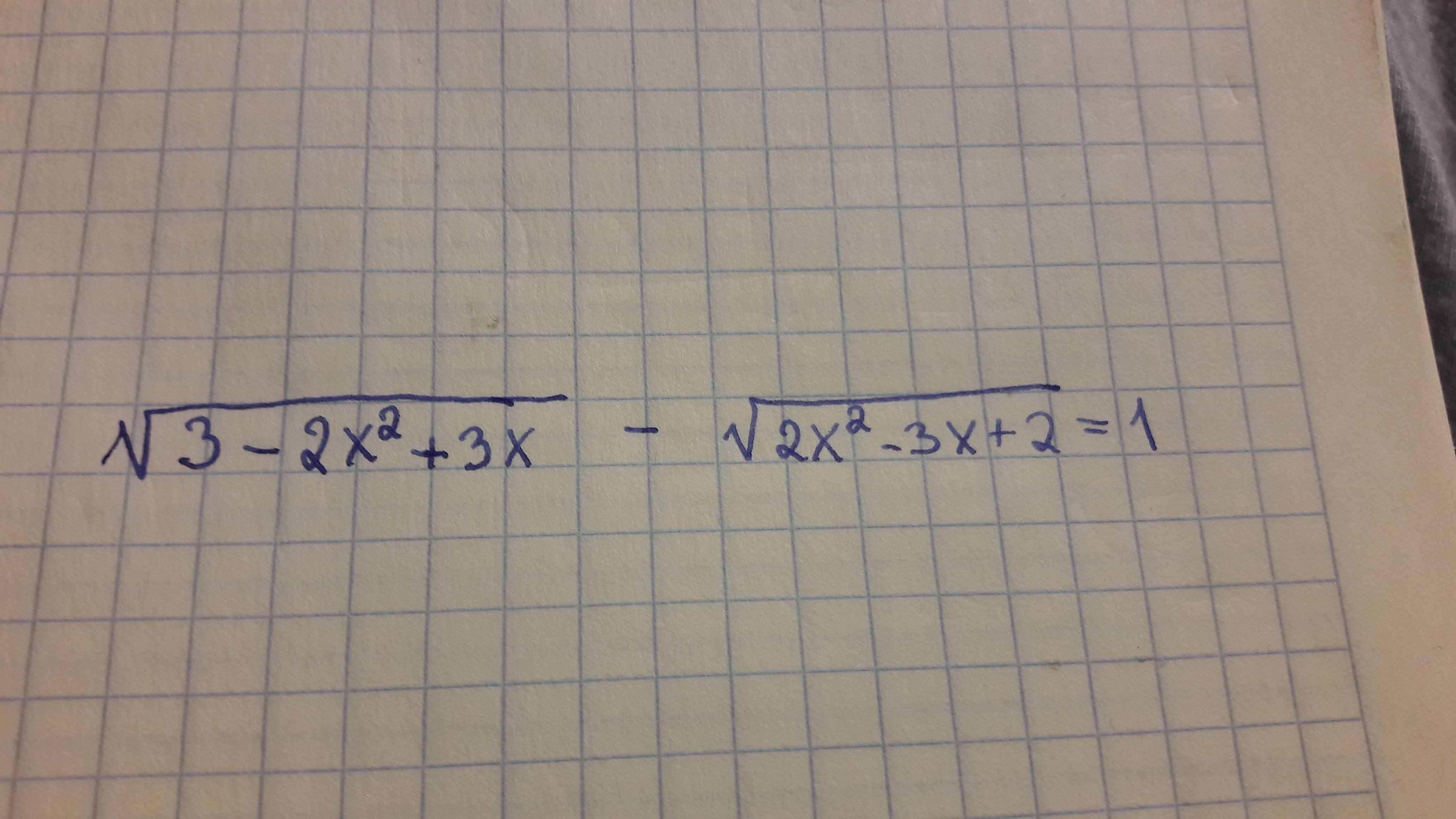
Ответы
Автор ответа:
0
√(3 - 2x² + 3x) - √(2x² - 3x +2) = 1
одз не будем ставить здесь видно что не больше 4-х решений и потом их проверим
замена 2x² - 3x +2 = t
3 - 2x² + 3x = 5 - (2x² - 3x + 2) = 5-t
√(5 -t) - √t = 1
√(5- t) = 1 + √t
5 - t = 1 + 2√t + t
2√t = 4 - 2t
√t = 2 - t
t = 4 - 4t + t²
t² - 5t + 4 = 0
D=35 - 16 = 9 =3²
t12= (5+-3)/2= 1 4
2x² - 3x +2 = t
2x² - 3x +2 = 1
2x² - 3x +1 = 0
D= 9 - 8 = 1
x12=(3+-1)/4 = 1 1/2
проверяем
√(3 - 2 + 3) - √ (2 - 3 +2) = √4 - √1 = 2 - 1 = 1 Да
√(3 - 2*1/4 + 3*1/2) - √(2*1/4 - 3/2 + 2) = √(3 - 1/2 + 3/2) - √(1/2 - 3/2 + 2) = √4 - √1 = 2 - 1 = 1 Да
2x² - 3x +2 = 4
2x²-3x-2=0
D=9 + 16 = 25 = 5²
x34=(3+-5)/4 = 2 -1/2
проверяем
√(3-2*4+3*2) - √(2*4 - 3*2 + 2) = √1 - √4 = 1 - 2 = -1 НЕт
√(3 - 2*1/4 - 3/2) - √(2*1/4 + 3/2 + 2) = √(3 - 1/2-3/2) - √(1/2 + 3/2 + 2) = 1 - 2 =-1 Нет
Ответ 1 1/2
одз не будем ставить здесь видно что не больше 4-х решений и потом их проверим
замена 2x² - 3x +2 = t
3 - 2x² + 3x = 5 - (2x² - 3x + 2) = 5-t
√(5 -t) - √t = 1
√(5- t) = 1 + √t
5 - t = 1 + 2√t + t
2√t = 4 - 2t
√t = 2 - t
t = 4 - 4t + t²
t² - 5t + 4 = 0
D=35 - 16 = 9 =3²
t12= (5+-3)/2= 1 4
2x² - 3x +2 = t
2x² - 3x +2 = 1
2x² - 3x +1 = 0
D= 9 - 8 = 1
x12=(3+-1)/4 = 1 1/2
проверяем
√(3 - 2 + 3) - √ (2 - 3 +2) = √4 - √1 = 2 - 1 = 1 Да
√(3 - 2*1/4 + 3*1/2) - √(2*1/4 - 3/2 + 2) = √(3 - 1/2 + 3/2) - √(1/2 - 3/2 + 2) = √4 - √1 = 2 - 1 = 1 Да
2x² - 3x +2 = 4
2x²-3x-2=0
D=9 + 16 = 25 = 5²
x34=(3+-5)/4 = 2 -1/2
проверяем
√(3-2*4+3*2) - √(2*4 - 3*2 + 2) = √1 - √4 = 1 - 2 = -1 НЕт
√(3 - 2*1/4 - 3/2) - √(2*1/4 + 3/2 + 2) = √(3 - 1/2-3/2) - √(1/2 + 3/2 + 2) = 1 - 2 =-1 Нет
Ответ 1 1/2
Похожие вопросы
Предмет: Литература,
автор: ruslangreciskin
Предмет: Другие предметы,
автор: kotkovnikita73
Предмет: Оʻzbek tili,
автор: nigorashagazatova
Предмет: Математика,
автор: незнайка4381
Предмет: Обществознание,
автор: Alin1010