Предмет: Информатика,
автор: igor11122
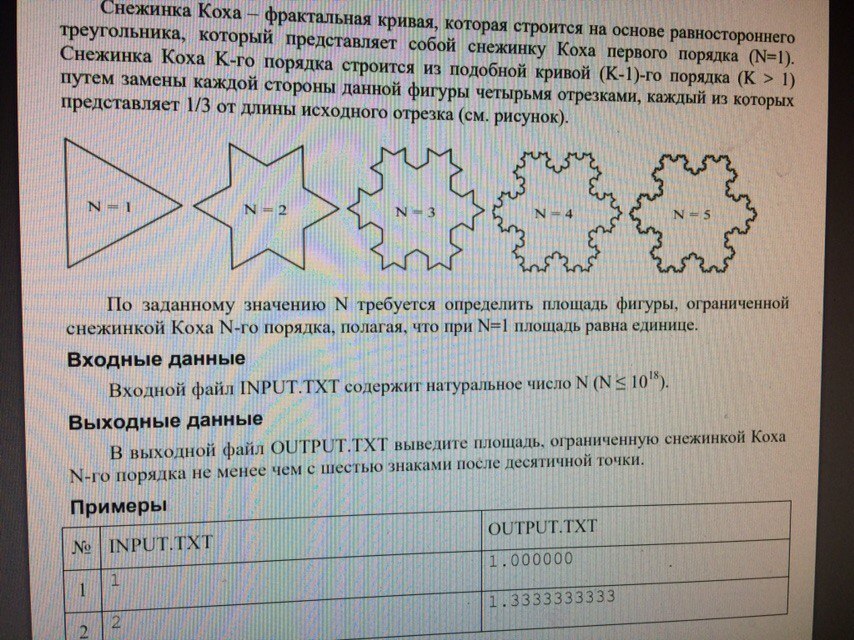
Помогите срочно с задачей по информатики (С++), БУДУ ОЧЕНЬ БЛАГОДАРЕН
Приложения:
Ответы
Автор ответа:
0
Пусть на k-м шаге длина сторон снежинки равна Ak, количество сторон Nk, тогда N1 = 3. На каждом шаге N увеличивается в 4 раза, A уменьшается в 3 раза, значит, Nk = 3 * 4^(k - 1), Ak = A1 / 3^(k - 1).
Будем следить за площадью. На (k + 1)-м шаге к площади добавляется Nk = 3 * 4^(k - 1) треугольников со стороной Ak / 3 = A1 / 3^k. Так как площадь треугольника со стороной A1 равна 1, то площадь каждого добавившегося треугольника 1/9^k, их добавилось 3/4 * 4^k, значит, на (k + 1)-м шаге добавляется площадь 3/4 * (4/9)^k.
Итак, площадь на n-м шаге равна Sn = 1 + 3/4 * 4/9 + 3/4 * (4/9)^2 + ... + 3/4 * (4/9)^(n - 1) = 1/4 + 3/4 * (1 + 4/9 + (4/9)^2 + ... + (4/9)^(n - 1))
В скобках стоит геометрическая прогрессия, её сумму можно посчитать по формуле.
Sn = 1/4 + 3/4 * (1 - (4/9)^n) / (5/9) = 1.6 - 1.35 * (4/9)^n
Ну и последнее наблюдение: вычислять Sn при всех n необязательно, второе слагаемое очень быстро стремится к нулю, и уже при n >= 19 второе слагаемое можно считать нулём. При остальных n степени можно считать как угодно, на скорость это значительно не повлияет.
#include <iostream>
#include <iomanip>
using namespace std;
int main() {
unsigned long long int n = 0;
float answer = 1.6;
cin >> n;
if (n <= 18) {
float power = 1;
while (n > 0) {
power *= 4./9;
n--;
}
answer -= 1.35 * power;
}
cout << fixed << setprecision(6) << answer;
return 0;
}
Будем следить за площадью. На (k + 1)-м шаге к площади добавляется Nk = 3 * 4^(k - 1) треугольников со стороной Ak / 3 = A1 / 3^k. Так как площадь треугольника со стороной A1 равна 1, то площадь каждого добавившегося треугольника 1/9^k, их добавилось 3/4 * 4^k, значит, на (k + 1)-м шаге добавляется площадь 3/4 * (4/9)^k.
Итак, площадь на n-м шаге равна Sn = 1 + 3/4 * 4/9 + 3/4 * (4/9)^2 + ... + 3/4 * (4/9)^(n - 1) = 1/4 + 3/4 * (1 + 4/9 + (4/9)^2 + ... + (4/9)^(n - 1))
В скобках стоит геометрическая прогрессия, её сумму можно посчитать по формуле.
Sn = 1/4 + 3/4 * (1 - (4/9)^n) / (5/9) = 1.6 - 1.35 * (4/9)^n
Ну и последнее наблюдение: вычислять Sn при всех n необязательно, второе слагаемое очень быстро стремится к нулю, и уже при n >= 19 второе слагаемое можно считать нулём. При остальных n степени можно считать как угодно, на скорость это значительно не повлияет.
#include <iostream>
#include <iomanip>
using namespace std;
int main() {
unsigned long long int n = 0;
float answer = 1.6;
cin >> n;
if (n <= 18) {
float power = 1;
while (n > 0) {
power *= 4./9;
n--;
}
answer -= 1.35 * power;
}
cout << fixed << setprecision(6) << answer;
return 0;
}
Похожие вопросы
Предмет: Математика,
автор: Dasha58780
Предмет: Химия,
автор: nasta778
Предмет: Математика,
автор: germanvorobev8
Предмет: История,
автор: AlexMiner1
Предмет: Литература,
автор: Кожевникова2004