Question

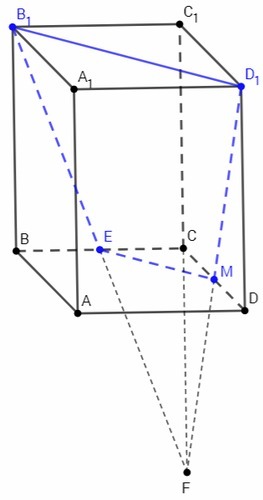
докажите что сечение правильного прямоугольного параллелепипеда АВСДА1В1С1Д1 проведенное через В1 Д1 и серединную точку М ребра ДС является равнобедренной трапецией
И постройте, пожалуйста

Answer 1

Грани призмы находятся в параллельных плоскостях. Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. B1D1 || EM, B1D1 || BD => EM || BD, EM - средняя линия △BCD, E - середина BC. Боковые грани правильного параллелепипеда - равные прямоугольники. B1E=D1M как соответствующие элементы равных прямоугольников. B1EMD1 - равнобедренная трапеция по определению.