Предмет: Геометрия,
автор: borisowskyleff
ДАЮ 20 БАЛЛОВ СРОЧНО ПОМОГИТЕ ПРОШУ!!!!!!!!!!!!!!!
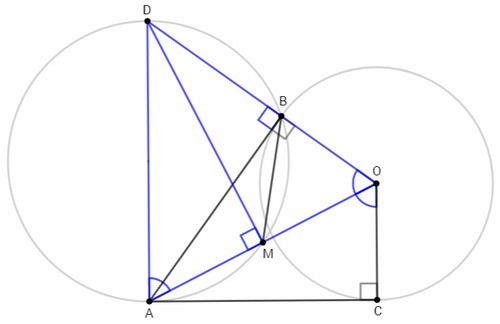
Из точки A провели касательные AB и AC к окружности с центром O (здесь B и C — точки касания). Точка M — середина отрезка AO. Докажите, что окружность, описанная около треугольника ABM, касается
прямой AC.
Ответы
Автор ответа:
0
AD - диаметр окружности, описанной около △ABM.
∠ABD=90 (опирается на диаметр)
∠ABO=90 (угол между касательной и радиусом)
∠DBO - развернутый, B∈DO
∠AMD=90 (опирается на диаметр), DM - высота △ADO
В треугольнике ADO высота является медианой =>
△ADO - равнобедреный, углы при основании равны, ∠DAO=∠AOD
△AOB=△AOC (прямоугольные с равными катетами и общей гипотенузой)*
∠AOD=∠AOC
∠DAO=∠AOC => AD||OC (накрест лежащие углы равны)
ОС⊥AC (радиус перпендикулярен касательной) => AD⊥AC
AC - касательная к окружности c диаметром AD.
-------------------------------------------------------------------
*) Треугольники, образованные отрезками касательных из одной точки, радиусами и отрезком, соединяющим точку и центр окружности, равны как прямоугольные (радиус перпендикулярен касательной) с равными катетами (радиусы) и общей гипотенузой.
∠ABD=90 (опирается на диаметр)
∠ABO=90 (угол между касательной и радиусом)
∠DBO - развернутый, B∈DO
∠AMD=90 (опирается на диаметр), DM - высота △ADO
В треугольнике ADO высота является медианой =>
△ADO - равнобедреный, углы при основании равны, ∠DAO=∠AOD
△AOB=△AOC (прямоугольные с равными катетами и общей гипотенузой)*
∠AOD=∠AOC
∠DAO=∠AOC => AD||OC (накрест лежащие углы равны)
ОС⊥AC (радиус перпендикулярен касательной) => AD⊥AC
AC - касательная к окружности c диаметром AD.
-------------------------------------------------------------------
*) Треугольники, образованные отрезками касательных из одной точки, радиусами и отрезком, соединяющим точку и центр окружности, равны как прямоугольные (радиус перпендикулярен касательной) с равными катетами (радиусы) и общей гипотенузой.
Приложения:
Похожие вопросы
Предмет: Химия,
автор: filimonovvladik616
Предмет: Литература,
автор: smg92838
Предмет: Математика,
автор: wqqxd
Предмет: Геометрия,
автор: Сара5642
Предмет: Алгебра,
автор: anastasia199874