Question

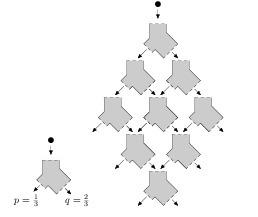
Дана вертикальная система трубок из пяти уровней, изображённая на рисунке, на каждом следующем трубка раздваивается. Сверху бросают шарик. Трубки устроены так, что из каждой он летит налево с вероятностью 1/3 и направо с вероятностью 2/3. Найдите вероятность того, что шарик достигнет нижней трубки. Ответ дайте с точностью до трёх знаков после запятой.

Answer 1

Рисунок к вопросу смотрите во вложении..

1) С верхней трубки двигаемся два раза направо и затем два раза налево, и принимая во внимая что события независимые, то вероятность независимых событий равна произведению вероятностей этих событий

$P_1=dfrac{2}{3}cdotdfrac{2}{3}cdotdfrac{1}{3}cdotdfrac{1}{3}$

2) Теперь двигаемся 1 раз направо; 1 раз налево; 1 раз направо и 1 раз налево, получим

$P_2=dfrac{2}{3}cdotdfrac{1}{3}cdotdfrac{2}{3}cdotdfrac{1}{3}$

3) 1 раз направо, 2 раза налево и 1 раз направо, получим вероятность третьего маршрута:

$P_3=dfrac{2}{3}cdotdfrac{1}{3}cdotdfrac{1}{3}cdotdfrac{2}{3}$

4) 1 раз налево; 2 раза направо; 1 раз налево, вероятность равна

$P_4=dfrac{1}{3}cdotdfrac{2}{3}cdotdfrac{2}{3}cdotdfrac{1}{3}$

5) 1 раз налево; 1 раз направо; 1 раз налево; 1 раз направо, получим вероятность:

$P_5=dfrac{1}{3}cdotdfrac{2}{3}cdotdfrac{1}{3}cdotdfrac{2}{3}$

6) 2 раза налево и 2 раза направо, вероятность такого маршрута, равна

$P_6=dfrac{1}{3}cdotdfrac{1}{3}cdotdfrac{2}{3}cdotdfrac{2}{3}$

Заметим, что вероятности всех шести маршрутов одинаковы, тогда по теореме сложения, искомая вероятность:

$P=P_1+P_2+P_3+P_4+P_5+P_6=6cdotdfrac{2}{3}cdotdfrac{2}{3}cdotdfrac{1}{3}cdotdfrac{1}{3}=dfrac{8}{27}approx0.296$

Ответ: 0,296.