Question

В треугольнике ABC стороны AB=10, AC=24, BC=26. В треугольнике проведены медианы AM и CN, точки M и N — середины сторон BC и AB, соответственно. Точка I лежит на стороне AC, при этом BI - биссектриса. Найдите площадь треугольника MNI

Answer 1

AN = NB
BM = MC
Т.е. MN - средняя линия треугольника ABC
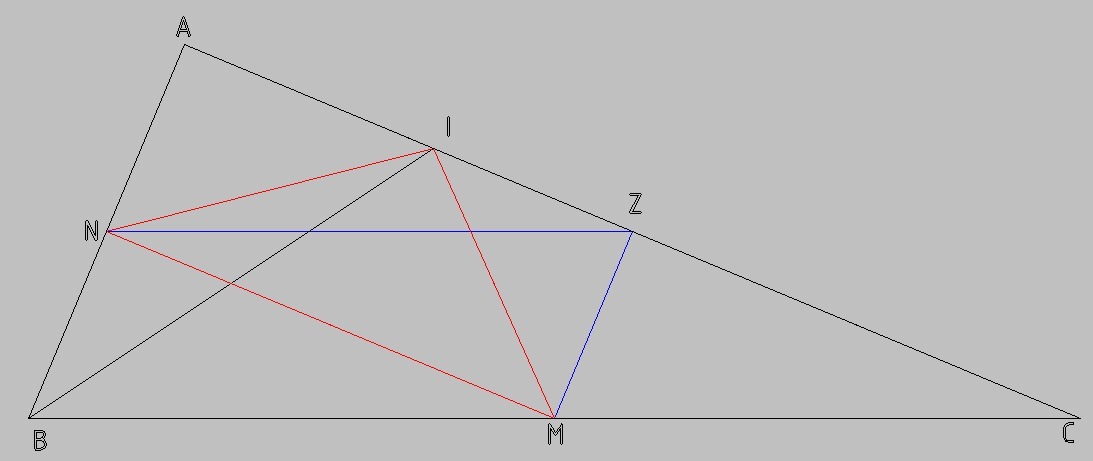
Построим вспомогательную точку Z, такую, что AZ = ZC
И NZ и MZ - средние линии треугольника ABC
Площадь треугольника, образованного средними линиями в четыре раза меньше площади исходного треугольника
S(ZNM) = 1/4 S(ABC)
Площадь треугольника INM равна площади треугольника ZNM, т.к. у них общее основание NM и одинаковая высота, равная расстоянию между параллельными прямыми NM и AC
S(INM) = S(ZNM) = 1/4 S(ABC)
Площадь исходного треугольника найдём по формуле Герона
$p=frac {a+b+c}{2}\ S = sqrt{p(p-a)(p-b)(p-c)}\ p=frac {10+24+26}{2} = 5+12+13 = 30\ S = sqrt{p(p-a)(p-b)(p-c)} = sqrt{30(30-10)(30-24)(30-26)}= \ = sqrt{30cdot20cdot6cdot4}=sqrt{120cdot120}=120$
S(INM) = 1/4 S(ABC) = 120/4 = 30