Question

Объясните,пожалуйста,Как это решать.Наклонная треугольная призма,в основании которой лежит правильный треугольник со стороной 3 корня из 3. Одна из вершин верхнего основания проектируется в центре нижнего основания.Боковые ребра составляют с плоскостью основания угол 60 градусов. Найдите объем призмы.

Answer 1

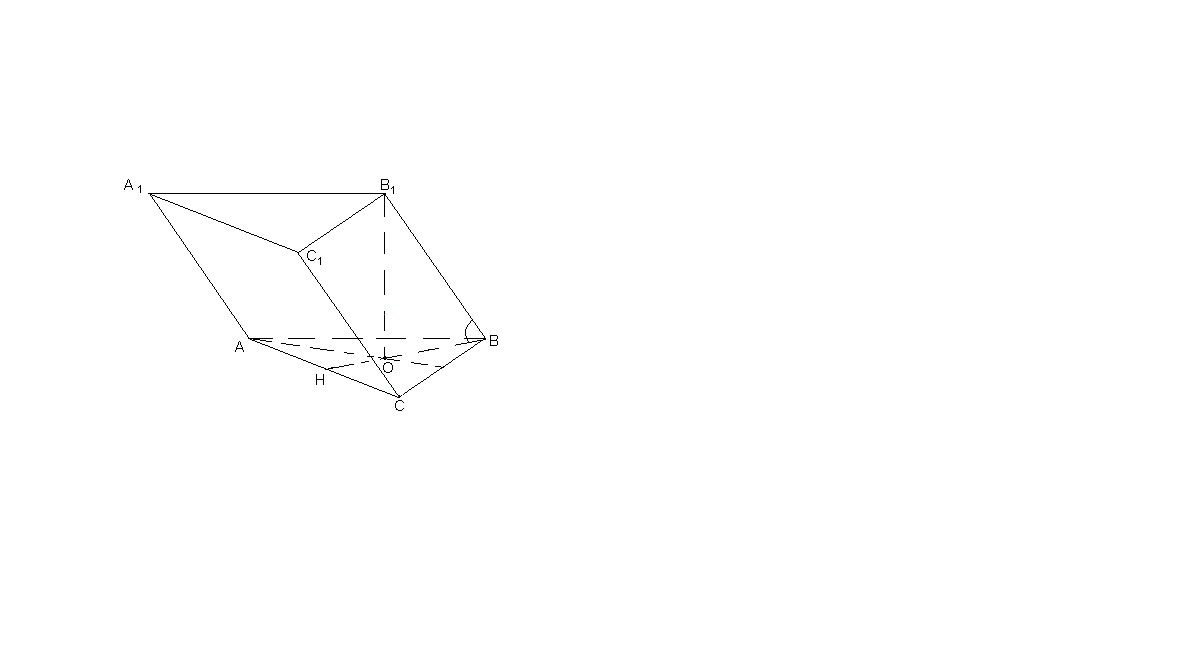
О - центр основания.
В₁О⊥АВС, тогда ВО - проекция ВВ₁ на плоскость основания.
Тогда ∠В₁ВО = 60° - угол наклона бокового ребра к основанию.
Объем любой призмы равен произведению площади основания на высоту:
V = Sосн · B₁O

Sосн = AB²√3 / 4 = (3√3)² · √3 / 4 = 27√3/4

BO = AB√3 / 3 как радиус окружности, описанной около правильного треугольника.
ВО = 3√3 · √3 / 3 = 3

ΔВ₁ОВ: ∠В₁ОВ = 90°,
               tg ∠B₁BO = B₁O/BO
               √3 = B₁O / 3
               B₁O = 3√3

V = 27√3/4 · 3√3 = 243/4