Question

В треугольнике ABC проведена медиана CM.
Найдите угол между двумя другими медианами, если AB=10, CM=15.
В ответе укажите градусную меру искомого угла.

Answer 1

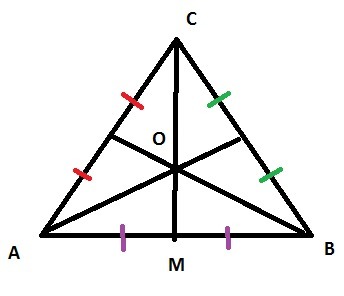
В Δ проведены 3 медианы, по свойству медиан в Δ знаем, что медиана в точке пересечения делится в соотношении 2:1, считая  от вершины, значит ОМ=СМ:3  ОМ=15:3=5см МВ=1/2АВ=10/2=5 см, так как СМ-медиана. 
ОМ=АМ=МВ, следовательно,  ∠МВО=∠МОВ, ∠МАО=∠АОМ, ∠АОВ=∠АОМ+∠МОВ, тогда х+х+2х=180°. 4х=180   х=45°⇒
∠АОВ=2х=2*45=90°
......................