Question

Периметр прямоугольника равен 68. Диагональ равна 7 см Найди периметр треугольника

Answer 1

Периметр прямоугольника P = 68см. Диагональ равна AC = 7см.
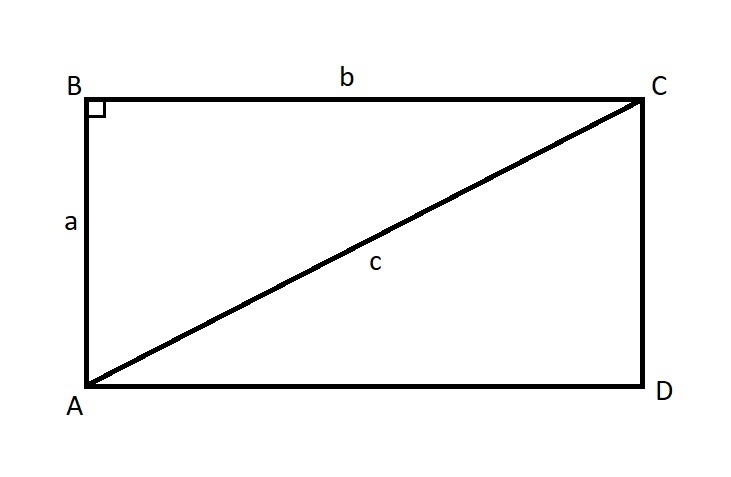
Пусть большая сторона прямоугольника равна b, меньшая равна a, а диагональ равна c. Тогда по теореме Пифагора можем записать, что:

$c^{2} = a^{2} + b^{2}$

Нам известна диагональ, она же гипотенуза, а любую из сторон можно выразить через другую зная периметр. Выразим, например, сторону a через сторону b:

$P = 2(a+b) = 68 \ \ a+b=34 \ \ a=34-b$

Тогда, можем записать, что:

$c^{2} = (34-b)^{2} + b^{2}$

Зная, что c = AC = 7:

$7^{2} = (34-b)^{2} + b^{2}$

$49 = 34^{2}-2cdot 34cdot b + b^{2} + b^{2}$

$49 = 34^{2}-68b + 2b^{2}$

$49 = 1156-68b + 2b^{2}$

$2b^{2} - 68b + 1107= 0$

$D=68^2 - 4cdot 2cdot 1107 = 4624 - 8856 textless 0$ - нет решений.