Предмет: Геометрия,
автор: polisavostina
В параллелограмме ABCD известно, что угол А=60 градусов, АВ =10 см, АD=16. Найдите расстояния от вершин В и D до биссектрисы угла BCD.
Ответы
Автор ответа:
0
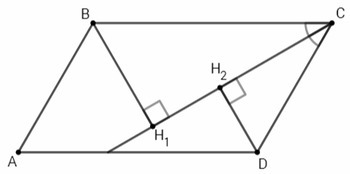
BH1, DH2 - перпендикуляры, опущенные на биссектрису угла С.
В параллелограмме противоположные стороны равны, противоположные углы равны.
BC=AD=16
CD=AB=10
∠С=∠A=60°
Биссектриса делит угол пополам.
∠BСH1=∠DCH2=∠С/2=60°/2=30°
Катет, лежащий против угла 30°, равен половине гипотенузы.
BH1=BC/2=16/2=8
DH2=CD/2=10/2=5
В параллелограмме противоположные стороны равны, противоположные углы равны.
BC=AD=16
CD=AB=10
∠С=∠A=60°
Биссектриса делит угол пополам.
∠BСH1=∠DCH2=∠С/2=60°/2=30°
Катет, лежащий против угла 30°, равен половине гипотенузы.
BH1=BC/2=16/2=8
DH2=CD/2=10/2=5
Приложения:
Похожие вопросы
Предмет: История,
автор: krissmeisarosh
Предмет: Математика,
автор: ulbosyntazikenova
Предмет: Другие предметы,
автор: djovanni12
Предмет: Химия,
автор: Аноним
Предмет: Математика,
автор: Аноним