Предмет: Алгебра,
автор: КилоЛеденцов
решите уравнение 4sin^4(2x)+16cos^4(2x)=5
Приложения:
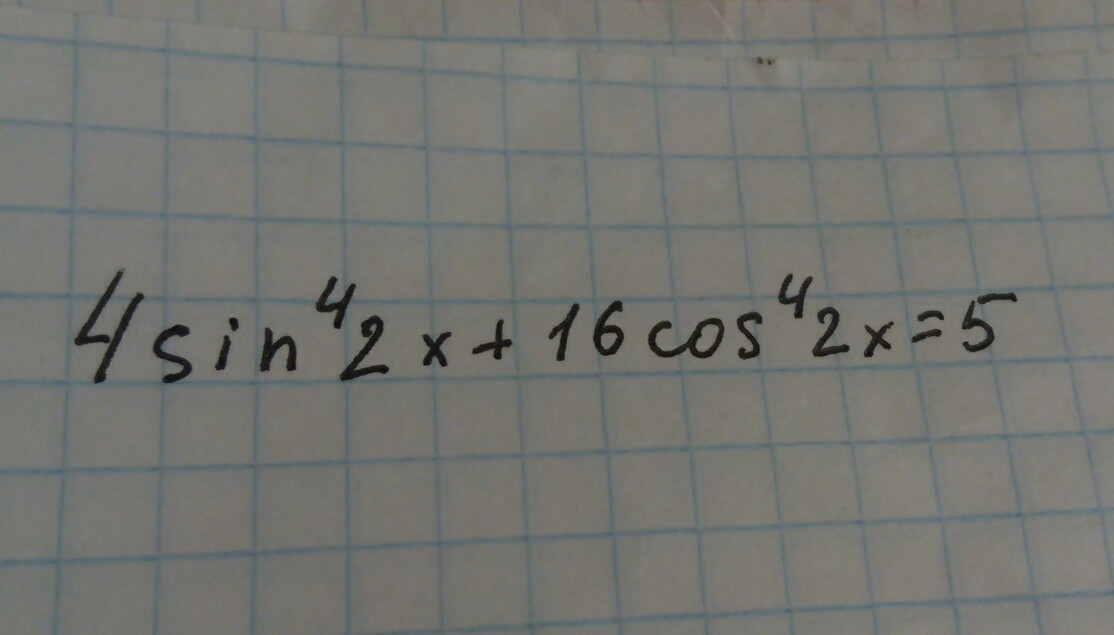
Ответы
Автор ответа:
0
Разложим косинус 4х как косинус двойного угла 2х.
Применим формулу cos2a = 1- 2 sin^2 a .
4 sin^4(2x) +3( 1 - 2 sin^2(2x)) -1 =0;
4sin^4(2x)-6 sin^2(2x) +2=0;
2 sin^4(2x) - 3 sin^2(2x)+ 1 =0;
sin^2(2x)=t; 0≤t ≤1;
2 t^2 - 3t +1=0;
t1=1; ⇒ sin^2(2x)=1; ⇒ sin 2x = + -1;
⇒2x= pi/2 + pik;k∈Z. ⇒x=pi/4 + pik/2.
t2= 1/2;⇒ sin^2(2x)=1/2;⇒ sin(2x) = +-sgrt2/2;⇒
⇒2x= pi/4 +pi/2*k. ⇒x= pi/8 + pik/4.
Применим формулу cos2a = 1- 2 sin^2 a .
4 sin^4(2x) +3( 1 - 2 sin^2(2x)) -1 =0;
4sin^4(2x)-6 sin^2(2x) +2=0;
2 sin^4(2x) - 3 sin^2(2x)+ 1 =0;
sin^2(2x)=t; 0≤t ≤1;
2 t^2 - 3t +1=0;
t1=1; ⇒ sin^2(2x)=1; ⇒ sin 2x = + -1;
⇒2x= pi/2 + pik;k∈Z. ⇒x=pi/4 + pik/2.
t2= 1/2;⇒ sin^2(2x)=1/2;⇒ sin(2x) = +-sgrt2/2;⇒
⇒2x= pi/4 +pi/2*k. ⇒x= pi/8 + pik/4.
Похожие вопросы
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: lybovaa
Предмет: Алгебра,
автор: mpankrateva905
Предмет: История,
автор: nikolayvazhnov