Предмет: Математика,
автор: ТвояМилая
Помогите пожалуйста задание 10 11 12
Приложения:
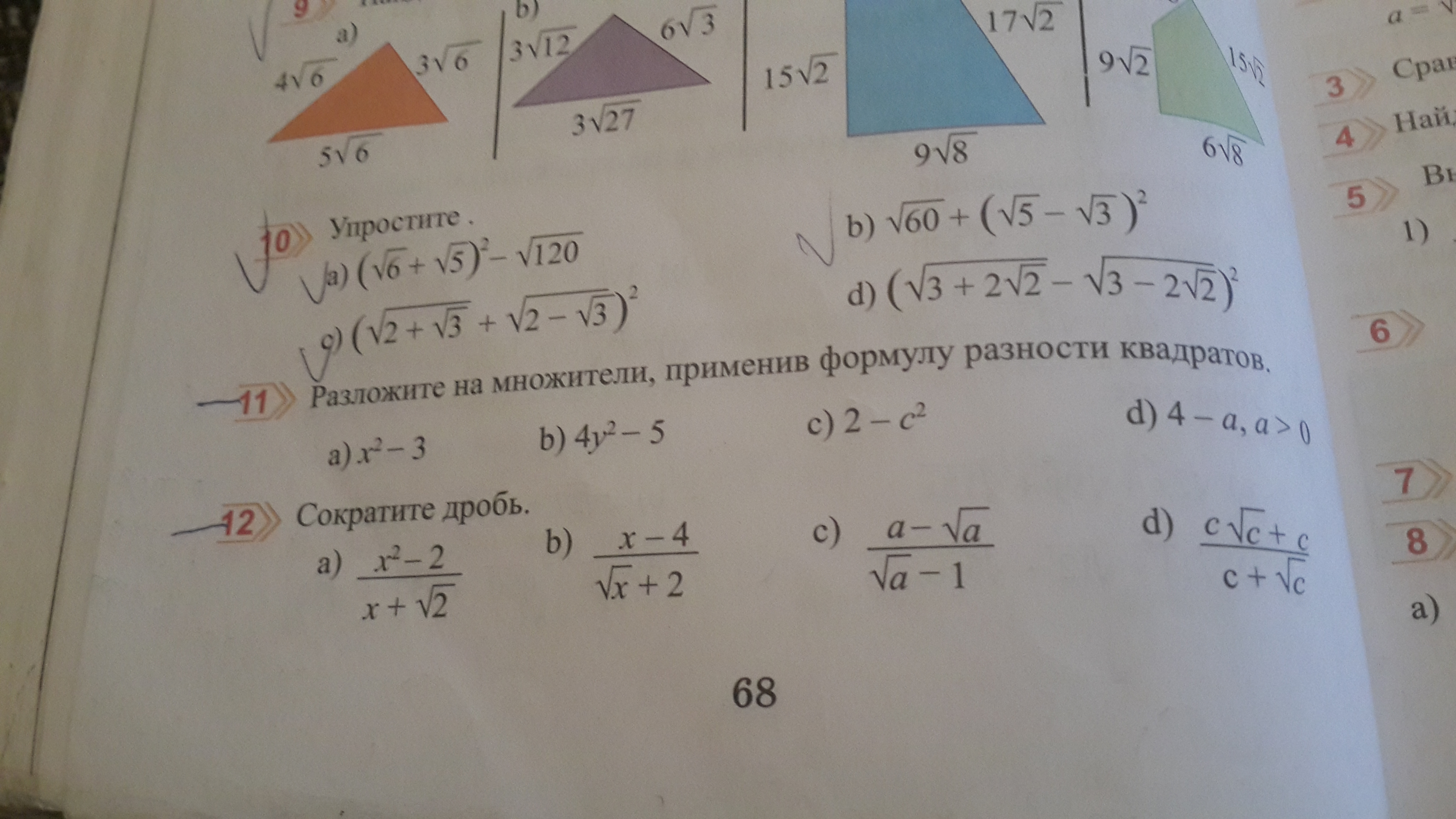
Ответы
Автор ответа:
0
ЗАПОМИНАЕМ (на всю жизнь)
1) √a * √a = a
2) √a*√b = √(a*b)
3) a*√b = √(a²*b)
РЕШЕНИЕ
10.
a) Квадрат суммы
(√6 + √5)² = 6 + 2*√(6*5) + 5 = 11 + √4*6*5) = 11 + √120
ОТВЕТ 11
b) Квадрат разности.
√60 - (5 - 2*√(3*5)+5) = √60 - √(4*15) = 0 - ОТВЕТ
с) Квадрат суммы и разность квадратов
(2+√3 + 2*(4-3) + 2 - √3) = 4 + 2 = 6 - ОТВЕТ
d) самостоятельно.
11.
а) (x-√3)*(x+√3) - ОТВЕТ
b) (2*y -√5)*(2*y+√5) - ОТВЕТ
c) (√2-c)(√2+c) -ОТВЕТ
d) (2 - √a)*(2+√a) - ОТВЕТ
12.
а) (x-√2)*(x+√2)/(x+√2) = x-√2 - ОТВЕТ
b) (√x - 2)(√x + 2)/ (√x + 2) = √x - 2 - ОТВЕТ
с) Избавляемся от корней в знаменателе. Умножаем на = √а + 1.
(a-√a)*(√a - 1)/(a-1) = (a*√a -a +√a² + √a) /(a-1) = √a*(a+1)/(a-1)
1) √a * √a = a
2) √a*√b = √(a*b)
3) a*√b = √(a²*b)
РЕШЕНИЕ
10.
a) Квадрат суммы
(√6 + √5)² = 6 + 2*√(6*5) + 5 = 11 + √4*6*5) = 11 + √120
ОТВЕТ 11
b) Квадрат разности.
√60 - (5 - 2*√(3*5)+5) = √60 - √(4*15) = 0 - ОТВЕТ
с) Квадрат суммы и разность квадратов
(2+√3 + 2*(4-3) + 2 - √3) = 4 + 2 = 6 - ОТВЕТ
d) самостоятельно.
11.
а) (x-√3)*(x+√3) - ОТВЕТ
b) (2*y -√5)*(2*y+√5) - ОТВЕТ
c) (√2-c)(√2+c) -ОТВЕТ
d) (2 - √a)*(2+√a) - ОТВЕТ
12.
а) (x-√2)*(x+√2)/(x+√2) = x-√2 - ОТВЕТ
b) (√x - 2)(√x + 2)/ (√x + 2) = √x - 2 - ОТВЕТ
с) Избавляемся от корней в знаменателе. Умножаем на = √а + 1.
(a-√a)*(√a - 1)/(a-1) = (a*√a -a +√a² + √a) /(a-1) = √a*(a+1)/(a-1)
Автор ответа:
0
Спасибо
Автор ответа:
0
а) (√6+√5)²-√120=(√6²+2√6√5+√5²)-√(4*30)=6+2√30+5-2√30=11
б) √60+(√5-√3)²=√(4*15)+(√5²-2√5√3+√3²)=2√15+5-2√15+3=8
в)


г)


х²-3=(х+√3)(х-√3)
4у²-5=(2у+√5)(2у-√5)
2-с²=(√2+с)(√2-с)
4-а=(2+√а)(2-√а)




б) √60+(√5-√3)²=√(4*15)+(√5²-2√5√3+√3²)=2√15+5-2√15+3=8
в)
г)
х²-3=(х+√3)(х-√3)
4у²-5=(2у+√5)(2у-√5)
2-с²=(√2+с)(√2-с)
4-а=(2+√а)(2-√а)
Автор ответа:
0
Спасибо
Похожие вопросы
Предмет: Математика,
автор: aluashka0208
Предмет: История,
автор: kseniakirichenko
Предмет: Українська мова,
автор: veronikalodge05
Предмет: Физика,
автор: PeTrUhAn4iK
Предмет: Литература,
автор: SonikX5000